多目标跟踪笔记一：Finding the Best Set of K Paths Through a Trellis With Application to Multitarget Tracking

Abstract

　　本文提出一种寻找K最优路径的方法。

　　k最优路径的定义：1.the sum of the metrics of all k paths in the set is minimized. 2.no two paths pass through a common state.

　　适用条件：M_i ≥ k （i = 0,1,2,......,N），M_i是第i层的state的数量；includes measurement errors and false alarm, but does not include the effeck of missing detections or merged measurements.
Algorithm 1：Viterbi Algorithm（K=1的特殊情况）

　　1）初始化第0层的所有state metrics为0；

　　2）for i = 1,2,3......N

　　　　　　计算i-1层的state metrics与i-1层到i层的branch metrics的和。对于i层的每个state，按照和的值最小的的要求确定i-1层到i层的连接，并以最小的和值最为i层的state metrics。

　　3）在N层，在所有state中选择state metrics值最小的，即可确定成本最优路径。

Algorithm 2：M₀ = M₁ = ...... = M_N = k情况下求解k最优路径

　　1）for i = 1,2,3......N

　　　　　　遍历i-1层到i层的K!个可能的连接方式，在这K!个连接方式中选择sum of k branch metrics最小的方式最为i-1层到i层的连接方式。（i-1层到i层的连接方式可能存在多种）

　　2）把i-1层到i层（i = 1,2,3......N）的连接方式串联起来就是k最优路径。

Algorithm 3：一般情况  M_i ≥ k ≥ 1

　　1）for i = 1,2,3......N

　　　　　　for j = 1,2,......,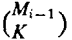

　　　　　　　　for k = 1,2,......,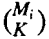

　　　　　　　　　　遍历i-1层到i层的K!个可能的连接方式，在这K!个连接方式中选择sum of k branch metrics最小的方式最为i-1层到i层的连接方式。

　　2）新建一个trellis，在第i层具有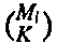个state；把1）中求得的连接方式（带有i-1层k个state到i层k个state的对应关系）作为branch。

　　3）针对这个新的trellis，利用Viterbi Algorithm算法求解k最优路径。

估计目标数量（轨迹数量）：

　　如果我们假设的目标数量一旦大于实际目标数量，很大可能最优路径的成本会出现激增的情况。

本文方法的局限性：

　　不能处理漏检（missed measurements）、遮挡（或者说一个measurement对应多个target的情况）、多传感器数据的情况等。