OO第三单元总结—

写在前面

OO的第三单元学习结束了，本单元我们学习了如何使用JML语言来对我们的程序进行规格化设计。并对openjml以及JMLUnitNG、JUnit等工具的使用有了初步的了解。

JML理论基础

注释结构

JML以javadoc注释的方式来表示规格，每行都以@起头。

JML表达式

JML表达式有一下几种：

原子表达式：如\result，\old等。
量化表达式：如\forall，\exists等。
集合表达式：这个不怎么常用，比如new JMLObjectSet {Integer i | s.contains(i) && 0 < i.intValue()}。
操作符：常用的包括等价关系<==>，推理关系==>，变量引用\nothing等。

JML方法规格

前置条件：通过\requires P表示，是对方法调用者的要求，意思是调用者确保P为真。
后置条件：通过\ensures P表示，是对方法实现者的要求，意思是方法实现者确保方法执行返回结果一定满足谓词P的要求，即确保P为真。
副作用范围限定：通过\assignable x表示，其中x为此方法可以更改的对象，极端情况为\nothing或\everything。
signals子句：一般用来限制抛出异常的条件。

JML类型规格

不变式invariant：是要求方法在所有可见状态下都必须满足的特性。
状态变化约束constraint：是要求对象的状态在变化时也要满足的约束。

JML工具链

使用OpenJML对实现的代码进行检查：包括JML语法静态检查，代码静态检查，运行时检查。
使用JMLUnitNG根据JML语言自动生成TestNG测试。

JMLUnitNG的使用

针对如图的compare方法，利用JMLUnitNG生成测试样例：

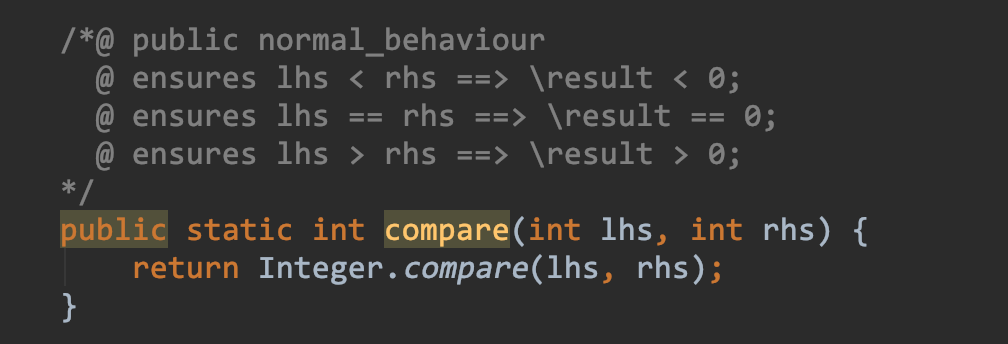
生成的样例点：

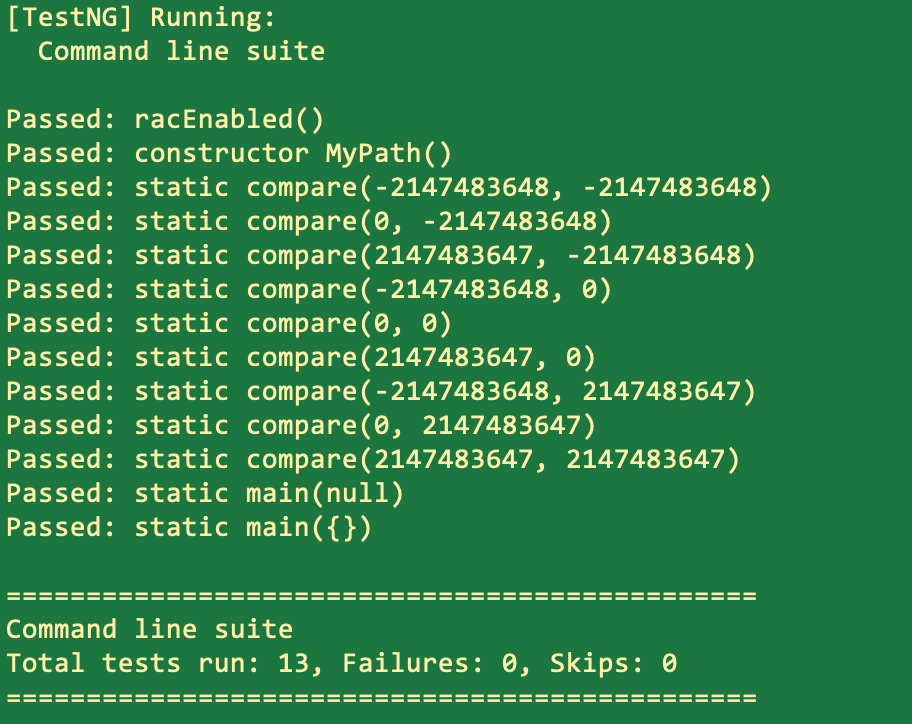
可以看到，自动生成的样例点对方法的各种边界情况进行了测试，包括正数和正数，正数和负数，负数和负数，还有0的情况，如果我们写的方法出现了加减法溢出的问题，这些测试样例也都会检测出来并报Failed。

架构设计

第九次作业

本次作业主要内容是实现Path和PathContainer，其中主要的查询方法是不同节点数的个数，我使用了均摊策略，即把查询的时间复杂度平均到addPath和removePath中，每次添加或删除路径时更近存放节点的HashMap，这样可以实现O(1)复杂度的查询方法。

第十次作业

本次作业是实现Path和Gragh，而Gragh是继承了PathContainer的，所以我在写的时候也使用了继承。本次作业的主要查询方法是最短路径，所以我重写了PathContainer里面的addPath和removePath方法，在添加删除路径的时候重新建图，并更新最短路径。对于PathContainer里面的其他方法，直接继承使用。

本次作业我使用的方法：

Floyd多源最短路算法
HashMap嵌套实现邻接矩阵的存储

第十一次作业

本次作业是实现Path和RaiwaySystem，其中RailwaySystem继承了Gragh。本次作业涉及到加权图以及换乘的代价，所以算法难度较大。在拓展的时候，我还是重写了addPath和removePath方法，并添加了几个方法来计算新的最短路问题。

本次作业我使用的方法：

分层的Floyd算法：即图结构变更之后，先对每条路径内部的点使用Floyd算法更新最短路，然后加上换乘代价，再对所有路径中的所有节点使用Folyd算法，即可实现带换乘代价的最短路算法。
静态数组存储结构：即用二维静态数组替代HashMap嵌套来实现邻接矩阵的存储，这样做的优点是计算速度，存取速度快，减少时间复杂度。缺点是不好维护和拓展。如果不是追求极致性能，还是慎用此类方法。
计算连通块的数量：使用并查集。

Bug分析

第九次作业

本次作业中，我的bug是减法溢出，具体是因为：我在实现compareTo方法的时候，采用的是两个整数相减来判断大小。而如果出现减法溢出的情况，那么判断结果跟正确答案是正好相反的。为此我也炸了强测+互测的20多个点。

本次作业中，同组同学的bug有：查询方法复杂度过高从而导致TLE，还有跟我一样的减法溢出问题。

第十次作业

本次作业中我的程序未被发现bug，我也未发现其他同学的bug

第十一次作业

本次作业中我的程序也未被发现bug，我也未发现其他同学的bug

心得体会

规格撰写方面

本单元让我体会到真正参与编写一个工程的感觉，即在一整个工程中分出一小部分让我们完成，并且要符合工程的要求。在这种情况下，JML语言体现出非常大的作用，它非常方便，不关注方法的实现过程，只专注于前因后果，因为只有前因后果才是把整个工程的思路贯穿起来的渠道。

此外，我也尝试过自己根据已有方法编写JML，也是有很大难度的，一定程度上，比我们写代码要难得多，这也体现出来规格化的重要性。

JUnit初体验

针对本单元各种小型模块的测试，我第一次使用了JUnit这个工具。可以说这个工具非常强大。如果说评测机是狂轰滥炸的飞弹，那么JUnit就是一把可以精确打击的匕首，也许你可以侥幸逃过狂轰滥炸，但是你绝对逃不过那精确一击。

一般JUnit测试所用样例都是自己精心构造的数据。随着代码不断完善进行补充。最方便的一点是：在每次版本更新后，都可以用JUnit一键回归测试，看是否改错了某些地方，可以说是非常强大的工具。

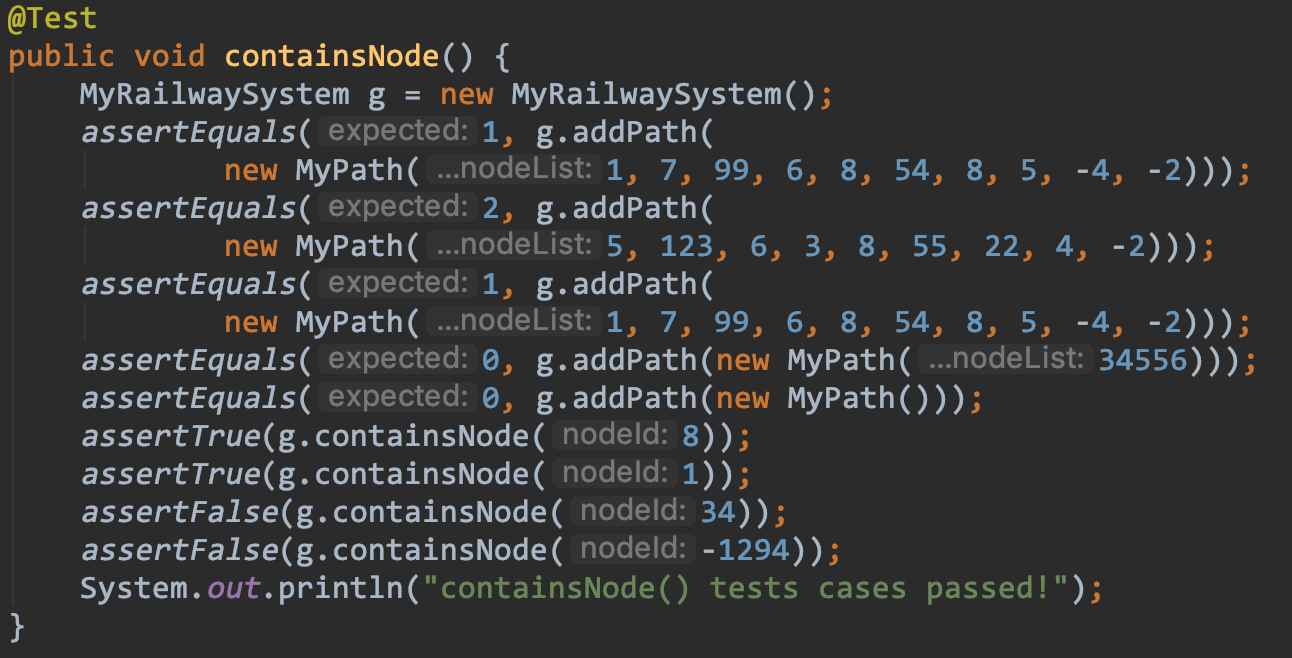
此外，JUnit还可以在运行的时候检测代码覆盖率，我们可以看到哪些地方被测试过，哪些地方还没有做测试，方便之后针对那些没有被覆盖的地方，继续补充测试样例。

OpenJML的使用

使用OpenJML工具可以对代码进行静态检查，有时候可以发现一些非逻辑错误导致的问题。比如我在第九次作业中出现的减法溢出的问题，其实是可以用OpenJML发现的，但当时对这种工具的使用还不是很了解，所以导致出现了bug。这也更加证明了在一个工程中，做好充分测试的必要性，不要让一个庞大的工程因为一个细小的错误而全盘崩塌。