[转帖]MerkleDAG全面解析 一文读懂什么是默克尔有向无环图

MerkleDAG全面解析 一文读懂什么是默克尔有向无环图

2018-08-16 15:58区块链/技术

MerkleDAG作为IPFS的核心数据结构，它融合了Merkle Tree和DAG的优点，今天阿信带大家一起来探究什么是MerkleDAG，拆分解说Merkle Tree、DAG有向无环图、MerkleDAG在IPFS中的应用。

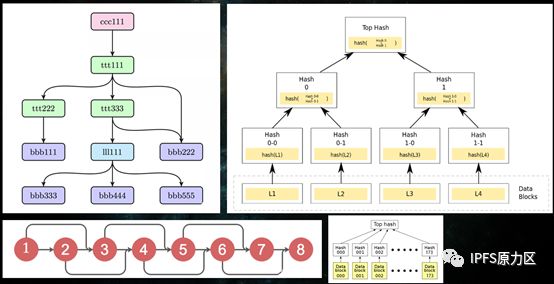
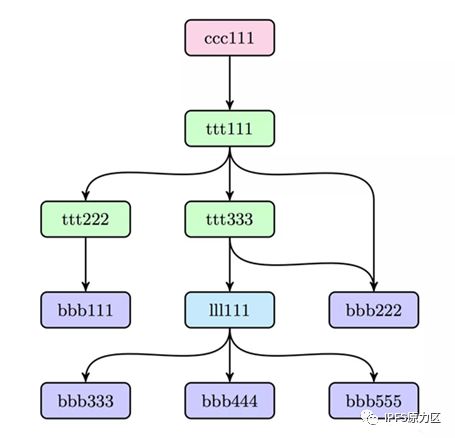MerkleDAG树形结构图

Merkle Tree

Merkle Tree是由美国计算机学家Merkle于1979年申请的专利。 Merkle Tree通常也被称作Hash Tree，顾名思义，就是存储hash值的一棵树。

1 那么，hash是什么

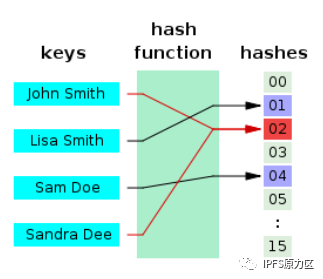• Hash是一个把任意长度的数据映射成固定长度数据的函数

• 输入数据的改变会得出不同的hash结果

2 Hash List

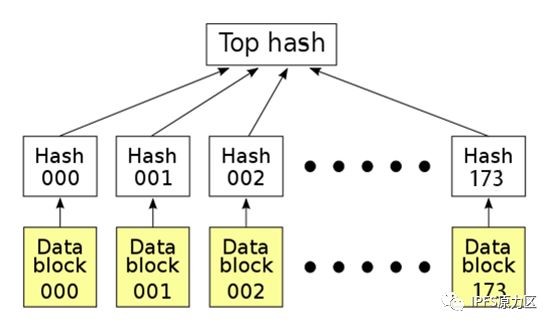点对点网络传输中，文件拆分，拆分后的小的数据块的hash组合成了hash list。 在传输过程中，如文件损坏了，只要重新下载损坏部分的数据块即可。

3 Merkle Tree

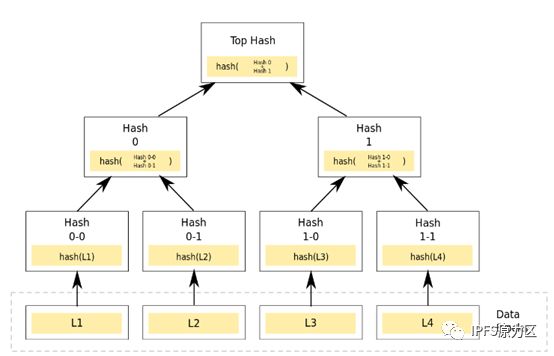• Merkle Tree大多数是二叉树，也可以多叉树；

• 叶子节点的value是数据集合的单元数据或者单元数据HASH；

• 非叶子节点的value是根据它下面所有的叶子节点值，然后按照Hash算法计算而得出的。

• 层层计算而形成的树形结构

DAG有向无环图

1 DAG起源

• 2013年，以色列希伯来学者在bitcointalik提出GHOST协议，引入DAG概念，作为比特币的交易处理能力扩容解决方案 • 随后，NXT社区提出用DAG的拓扑结构来存储区块 • 2015年9月，Sergio Demian Lerner发表了 《DagCoin: a cryptocurrency without blocks》。交易发起后，直接广播全网，跳过打包区块阶段。 • 2016年7月，IOTA横空出世，随后ByteBall也闪亮登场

2 DAG介绍

DAG 英文全称为：directed acyclic graph。 有向无环图，有方向无环路。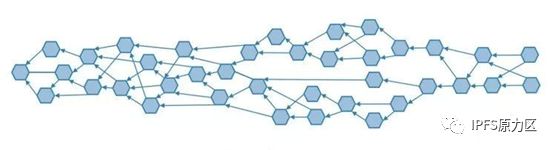假设当你发布新交易时，那么你的单元会主动同时链接到前面两个有效单元之中，DAG 中的每个新单元，验证并确认其父单元，以及父单元的父单元，慢慢可达创世单元，并将其父单元的哈希包含到自己的单元里面。 随着时间递增，所有交易单元相互连接，形成图状结构，如若要更改数据，那就不仅仅是几个单元数据的问题了，而是整个拓扑图的数据更改。DAG这个模式相比来说，要进行的复杂度更高，更难以被更改。区块链链式数据结构

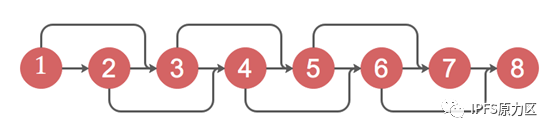DAG的拓扑数据结构

1和2号是创世单元；第3个单元产生时，只需要确认1号和2号的交易；第4个单元产生时，只需要确认2号和3号，以此类推。区块链的基础是分布式账本，而分布式账本的基础是分布式网络； 分布式账本是不是一定要是区块链呢？ 不一定，它还可以是DAG，也就是有向无环图，DAG不是区块链，当然你非要把它看成一条链也没毛病，但它是一条没有区块的链！

MerkleDAG

1 MerkleDAG功能

Merkle DAG拥有如下的功能：

• 内容寻址：使用多重哈希来唯一识别一个数据块的内容

• 防篡改：可以方便的检查哈希值来确认数据是否被篡改

• 去重：由于内容相同的数据块哈希是相同的，可以很容去掉重复的数据，节省存储空间

2 MerkleDAG树形结构构建过程

在IPFS网络中，存储文件时，首先会将文件切片，切割成256KB大小的文件。之后循环调用（MerkleDAG.Add）方法构建文件MerkleDAG。 文件hash值创建流程： 1：将切片之后的文件进行sha-256运算 2：将运算结果选取0~31位 3：将选取结果根据base58编码，运算结果前追加Qm 即为最后结果作为文件的46位hash值 根据IPFS底层代码计算，Merkle DAG为多叉树结构，最多为174叉树。

3 DAGService维护

在源代码之中通常使用DAGService维护MerkleDAG，为MerkleDAG提供删除和增加的权限，源代码如下：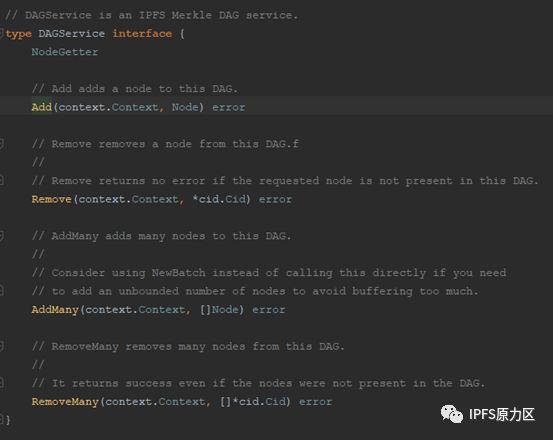

• 官网：http://ipfsforce.com
• 公众号：IPFS原力区
• 币快报社群：IPFS原力区
• 微博：http://weibo.com/ipfsforce

IPFS原力区

IPFS原力区是全球第一大IPFS价值生态社区，总部位于上海，聚集了众多技术大咖和IPFS爱好者；IPFS原力区秉持：价值，共建，共赢，荣耀的文化理念；提供全面、精细、优质的IPFS咨询和技术支持，将生态中的爱好者转化为IPFS支持者和参与者。 未来，IPFS原力区做好价值文化基因传播、紧盯人工智能，量子计算，大数据等前沿科技，把IPFS区块链技术随时架设在最新的技术基础之上，推动IPFS生态的健康发展。返回搜狐，查看更多