python 回溯法 子集树模板 系列 —— 14、最长公共子序列（LCS）

问题

输入

第1行：字符串A

第2行：字符串B

(A,B的长度 <= 1000)

输出

输出最长的子序列，如果有多个，随意输出1个。

输入示例

belong

cnblogs

输出示例

blog

分析

既然打算套用回溯法子集树模板，那就要祭出元素-状态空间分析大法。

以长度较小的字符串中的字符作为元素，以长度较大的字符串中的字符作为状态空间，对每一个元素，遍历它的状态空间，其它的事情交给剪枝函数！！！

解x的长度不固定，xi表示字符串b中的序号。

在处理每一个元素时，如果没有一个状态被选择（cnblogs中没一个字符被选取），那么程序无法去往下一个元素。

这确实是个不小的麻烦！！！思考了一天，终于想出办法了：扩充状态空间，增加一个状态q！如果元素选取了状态q，它是合法的。但是，状态q不加入解x内！！！

看一个直观的图：

至此，enjoy it!

代码

'''最长公共子序列'''

# 作者：hhh5460
# 时间：2017年6月3日

a = 'belong'
b = 'cnblogs'

x = []   # 一个解（长度不固定）xi是b中字符的序号
X = []   # 一组解

best_x = [] # 最佳解
best_len = 0 # 最大子序列长度

# 冲突检测
def conflict(k):
    global n, x, X, a,b,best_len

    # 如果两个字符不相等
    if x[-1] < len(b) and a[k] != b[x[-1]]:
        return True

    # 如果两个字符相等，但是相对于前一个在b中的位置靠前
    if a[k] == b[x[-1]] and (len(x) >= 2 and x[-1] <= x[-2]):
        return True

    # 如果部分解的长度加上后面a剩下的长度，小于等于best_len
    if len(x) + (len(a)-k) < best_len:
        return True

    return False # 无冲突

# 回溯法（递归版本）
def LCS(k): # 到达a中的第k个元素
    global x, X,a,b,best_len,best_x
    #print(k, x)
    if k == len(a):  # 超出最尾的元素
        if len(x) > best_len:
            best_len = len(x)
            best_x = x[:]
    else:
        for i in range(len(b)+1): # 遍历 状态空间：0~len(b)-1，技巧：人为增加一种状态len(b)，表示改行没有元素选取
            if i==len(b): # 此状态不放入解x内
                LCS(k+1)
            else:
                x.append(i)
                if not conflict(k): # 剪枝
                    LCS(k+1)
                x.pop()              # 回溯

# 根据一个解x，构造最长子序列lcs
def get_lcs(x):
    global b

    return ''.join([b[i] for i in x])

# 测试
LCS(0)
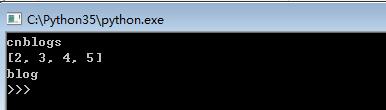
print(b)
print(best_x)
print(get_lcs(best_x))

效果图