【hihocoder】二分·归并排序之逆序对

描述

在上一回、上上回以及上上上回里我们知道Nettle在玩《艦これ》。经过了一番苦战之后，Nettle又获得了的很多很多的船。
这一天Nettle在检查自己的舰队列表：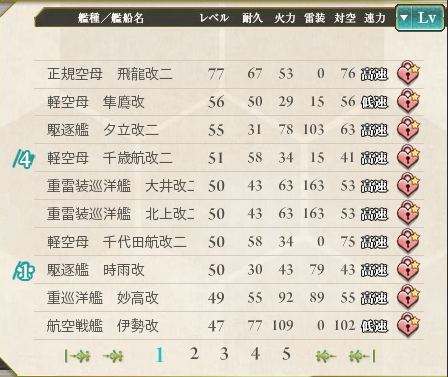

我们可以看到，船默认排序是以等级为参数。但实际上一个船的火力值和等级的关系并不大，所以会存在A船比B船等级高，但是A船火力却低于B船这样的情况。比如上图中77级的飞龙改二火力就小于55级的夕立改二。
现在Nettle将按照等级高低的顺序给出所有船的火力值，请你计算出一共有多少对船满足上面提到的这种情况。

提示：火力高才是猛！

输入

第1行：1个整数N。N表示舰船数量, 1≤N≤100,000
第2行：N个整数，第i个数表示等级第i低的船的火力值a[i]，1≤a[i]≤2^31-1。

输出

第1行：一个整数，表示有多少对船满足“A船比B船等级高，但是A船火力低于B船”。

样例输入

10
1559614248 709366232 500801802 128741032 1669935692 1993231896 369000208 381379206 962247088 237855491

样例输出

27

解题思路：归并排序是将数列a[l,h]分成两半a[l,mid]和a[mid+1,h]分别进行归并排序，然后再将这两半合并起来。在合并的过程中（设l<=i<=mid，mid+1<=j<=h），当a[i]<=a[j]时，并不产生逆序数；当a[i]>a[j]时，在前半部分中比a[i]大的数都比a[j]大，将a[j]放在a[i]前面的话，逆序数要加上mid+1-i。因此，可以在归并排序中的合并过程中计算逆序数.
注意范围，逆序数最大为n*(n-1)/2，结果用long long保存。

#include <stdio.h>

using namespace std;
const int N =  + ;

int a[N],tmp[N];
long long ans;

void Merge(int l,int m,int r)
{
    int i = l;
    int j = m + ;
    int k = l;
    while(i <= m && j <= r)
    {
        if(a[i] > a[j])
        {
            tmp[k++] = a[j++];
            ans += m - i + ;
        }
        else
        {
            tmp[k++] = a[i++];
        }
    }
    while(i <= m) tmp[k++] = a[i++];
    while(j <= r) tmp[k++] = a[j++];
    for(int i=l;i<=r;i++)
        a[i] = tmp[i];
}

void Merge_sort(int l,int r)
{
    if(l < r)
    {
        int m = (l + r) >> ;
        Merge_sort(l,m);
        Merge_sort(m+,r);
        Merge(l,m,r);
    }
}

int main()
{
    int n;
    //freopen("in.txt","r",stdin);
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=;i<n;i++)
            scanf("%d",&a[i]);
        ans = ;
        Merge_sort(,n-);
        printf("%lld\n",ans);
    }
    return ;
}