奇怪吸引子---ChenLee
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性、稳定性、吸引性。吸引子是一个数学概念,描写运动的收敛类型。它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它,这样的集合有很复杂的几何结构。由于奇怪吸引子与混沌现象密不可分,深入了解吸引子集合的性质,可以揭示出混沌的规律。
这里会展示利用奇怪吸引子生成的艺术图像。奇怪吸引子通常含有三维或四维的数据,而图像是二维的,因此可以从不同的位面将奇怪吸引子投影到二维图像中。
原图及数学公式取自:
http://chaoticatmospheres.com/125670/1204030/gallery/strange-attractors

这里使用自己定义语法的脚本代码生成混沌图像,相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815。
脚本代码:
[ScriptLines]
u=a*i - j*k
v=b*j + i*k
w=c*k + i*j/
i=i+u*t
j=j+v*t
k=k+w*t
x=i
y=j [Variables]
a=5.000000
b=-10.000000
c=-0.380000
i=-1.000000
j=-1.000000
k=-1.000000
t=0.001000
混沌图像:


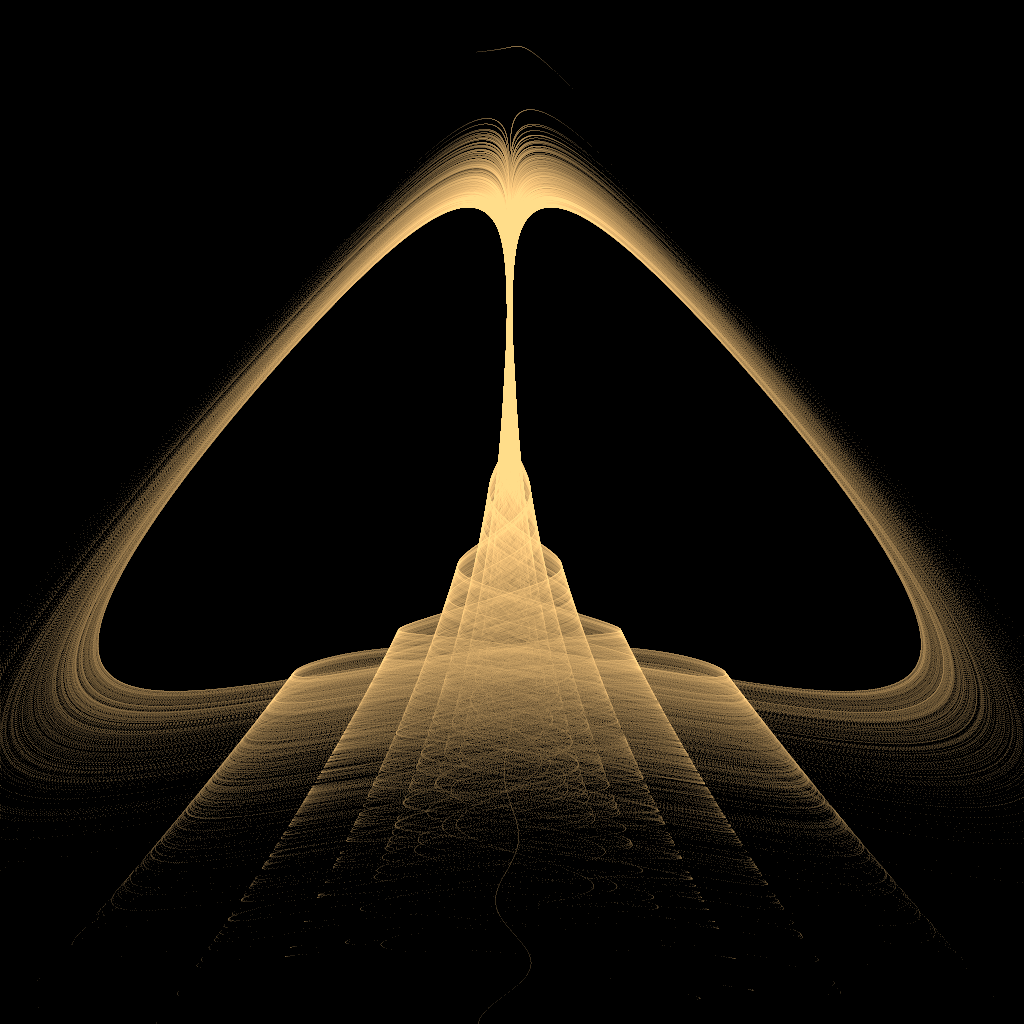
奇怪吸引子---ChenLee的更多相关文章
- 奇怪吸引子---YuWang
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WimolBanlue
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WangSun
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---TreeScrollUnifiedChaoticSystem
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Thomas
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---ShimizuMorioka
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Sakarya
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Russler
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Rucklidge
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
随机推荐
- JavaScript 的装饰器:它们是什么及如何使用
请访问我的独立博客地址:https://imsense.site/2017/06/js-decorator/ 装饰器的流行应该感谢在Angular 2+中使用,在Angular中,装饰器因TypeSc ...
- CentOS 7使用yum安装PHP5.6
删除旧php包 yum remove php.x86_64 php-cli.x86_64 php-common.x86_64 php-gd.x86_64 php-ldap.x86_64 php-mbs ...
- RabbitMQ消息交换模式简介
RabbitMQ是AMQP的一个典型实现,它消息发布者的消息发布到Exchange上,同时需要制定routingkey,可以通过指定交换机的不同模式实现不同的行为. RabbitMQ提供了四种Exch ...
- 交叉编译gdb和gdbserver
从http://ftp.gnu.org/gnu/gdb/下载最新的gdb,我下载的是gdb-8.0. 编译aarch32(>armv5): #!/bin/bash export CC=arm-n ...
- ASP.NET Web API基于OData的增删改查,以及处理实体间关系
本篇体验实现ASP.NET Web API基于OData的增删改查,以及处理实体间的关系. 首先是比较典型的一对多关系,Supplier和Product. public class Product { ...
- 使用Axure RP原型设计实践08,制作圆角文本框
本篇体验做一个简单圆角文本框,做到3个效果: 1.初始状态,圆角文本框有淡淡的背景色,边框的颜色为浅灰色2.点击圆角文本框,让其获取焦点,边框变成蓝色,背景色变成白色3.圆角文本框失去焦点,边框变成红 ...
- WCF中修改接口或方法名称而不影响客户端程序
本篇接着"从Web Service和Remoting Service引出WCF服务"中有关WCF的部分. 运行宿主应用程序. 运行Web客户端中的网页. 输入内容,点击按钮,能获取 ...
- jQuery统计上传文件的大小
对于现代浏览器(支持html5)来说,在客户端统计上传文件的大小,可以通过$(selector)[0].files[0].size来实现.但在老版本的IE浏览器中,比如IE7,IE8或IE9,却不支持 ...
- Time Zones And Daylight Savings Time
This page describes code for working with Time Zones and Daylight Savings Time. Neither VBA nor VB6 ...
- 使用jQuery实现图片懒加载原理
原文:https://www.liaoxuefeng.com/article/00151045553343934ba3bb4ed684623b1bf00488231d88d000 在网页中,常常需要用 ...
