EM算法理解

一、概述

概率模型有时既含有观测变量，又含有隐变量，如果概率模型的变量都是观测变量，那么给定数据，可以直接利用极大似然估计法或者贝叶斯估计法估计模型参数。但是，当模型同时又含有隐变量时，就不能简单地使用这些方法。EM算法适用于带有隐变量的概率模型的参数估计，利用极大似然估计法逐步迭代求解。

二、jensen不等式

  是区间 上的凸函数，则对任意的 ，有不等式：

 

即：

　　E[f(X)] ≥ f(E(X))  ,因为(x1+x2+...+xn)/n=E(X),同理可得E(f(X))。当x1=x2=...=xn的时候等式成立。

 

如果是凹函数，怎正好反过来。

 

假设f(x)=log(x),则根据jensen不等式可得：

因为log函数是一个凹函数，所以正好反过来，Σλ_jy_j就是变量Y的期望。后面会用到该log对应的jensen不等式，当y_i是一个固定常数的时候等式成立。

 

三、高斯混合模型求解

 

1）问题描述

　　还是以经典的身高为例子，假设有100个身高的数据集，这100个人由广东人和东北人组成，但是具体却不知道每个人来自哪里。假设广东人和东北人的身高分别符合某一参数的高斯分布，如何利用这100个人去评估求解广东人和东北人的分布参数呢？如果我们知道哪个人来自哪里，利用极大似然估计直接求解即可得到各自的分布参数；但是这里面不知道哪个人具体来自哪里，所以隐含了一个地域分布的变量，含有隐变量的情况下就不能直接利用MLE求解了，这个时候EM就可以发挥作用了。这两个人群混合在一起其实就是高斯混合模型，如下：

 

 其中，α_k是系数，α_k≥0，Σα_k=1；ø(x;θ_k)是高斯分布密度函数，θ_k=（μ_k,σ_k）。这里我们要求解的参数就是α_k和θ_k，P(x;θ)这个两个高斯分布的混合高斯模型。

 

2）公式推导

 我们把隐变量考虑进去，用z表示隐变量地域的分布，例如z=0表示来自广东，z=1表示来自东北，写出对应的似然函数如下：

 之所以后面按z累加概率，是因为在不知道一个样本来自哪里的情况下，就把可能出现的概率累加起来就是表示该样本出现的概率。

上面这个式子log后面是一个累加项，求导会非常麻烦，做一个转化，这里面要用到上面提到的jensen不等式，求一个近似的函数逼近原函数逐步求解：

 

 这里面的Q(z)就是关于z的分布函数，Q(z)≥0，∑Q(z)=1,根据上面的jensen不等式可得上述不等式。

 我们找到了似然函数的一个下界，如何去优化呢？我们首先必须保证这个下界是紧的，也就是至少要满足等号成立的条件。由Jensen不等式，等式成立的条件是随机变量是固定常数，也就是：

 

而满足该式子等于常数C的时候，我们的Q(z)到底是什么形式呢？如何求得Q(z)呢？往下看：

因为：

 

 

所以：

进而：

这个时候Q(z)我们就找到了，Q(z)就是在知道参数θ情况下，样本x_i属于z地域的概率值。

 

3）图形化展示优化思路

当我们初始化参数θ1的时候，带入公式会得到Q(z)的分布，这个时候的的Q(z)是满足等号成立的条件的，因为我们推导求Q(z)公式的时候就是按等号成立的条件去推导的。所以这个时候的下界函数和原似然函数L(θ)在θ1处值是相等的，下界函数的曲线就是图示中θ1与θ2所在的第一个黑色曲线。下一步我们优化下界函数，求得其极大值，就会得到如图所示的θ2的参数值。此时我们将θ2再次带入公式，得到一个新的Q(z)分布，Q(z)变了，当然下界函数曲线也变了，新的下界函数就是图示θ2和θ3所在的第二条黑色曲线，因为θ2带入Q(z)之后，这个时候跟θ1带入一样，是满足等式成立的条件的，所以新的黑色曲线就在θ2处上方与L(θ)值相等，接着求当前下界函数的极大值，得出θ3参数。如此下去，就能无限接近原似然函数的极值点。

 

4）算法具体步骤

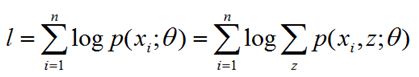
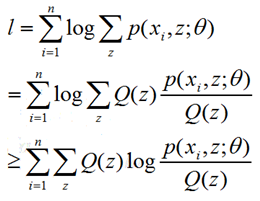
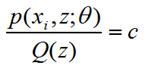
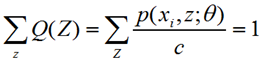
首先，初始化参数θ

　　（1）E-Step：根据已知参数θ计算每个样本属于z的概率，即这个身高来自广东或东北的概率，这个概率就是Q(z)，这一步为什么叫求期望呢？我的理解是这样的，下界函数是 ∑∑Q(z)*log(p(x,z;θ)/Q(z))，Q(z)本身就是一个概率分布，所以这正是求期望的公式。

　　（2）M-Step：根据计算得到的Q(z)，求出含有θ的似然函数的下界并最大化它，得到新的参数θ。这里面下界函数中，Q(z)带入初始化或者前一步已知的θ参数值，而p(xi,z;θ)中Θ参数还是未知，相当于成了以θ为变量的函数，这一步极大化求函数的极值点对应的θ点即可。

　　重复（1）和（2）直到收敛，可以看到，从思想上来说，和最开始没什么两样，只不过直接最大化似然函数不好做，曲线救国而已。

　　至于为什么这样的迭代会保证似然函数单调不减，即EM算法的收敛性证明，《统计学习方法》里面有证明。EM算法在一般情况是收敛的，但是不保证收敛到全局最优，即有可能进入局部的最优。

 

 

 

 

参考链接：https://www.cnblogs.com/bigmoyan/p/4550375.html

                  https://www.cnblogs.com/Gabby/p/5344658.html