拔靴法--Bootstrap--R语言实现
拔靴法属于重复抽样(resampling)方法,与Monte Carlo相比,二者真实的母体不同。它是将已有的观察值作为母体重复抽样,
以求取原先资料不足二无法探讨的资料特性。
举个例子,假设x1,x2,...,xn为来自同一分配的观察值,我们想了解这个分配的中位数。
设一组有Poisson分配抽出的随机样本,6 7 7 7 7 8 ... 15 15 17 20,共30个。已知样本中位数为10。
这里我们分别用MC方法和拔靴法模拟10000次,看中位数的分布。
# Monte Carlo
t1 = NULL
for (i in 1:10000){
x1=rpois(30,10);y1=median(x1);t1=c(t1,y1)
} # Bootstrap
t2 = NULL
x0 = rpois(30,10)
for (i in 1:10000){
x2=sample(x0,30,T);y2=median(x2);t2=c(t2,y2)
} par(mfrow=c(1,2)) hist(t1,xlab = "Median",main = "Monte Carlo")
hist(t2,xlab = "Median",main = "Bootstrap")
输出:
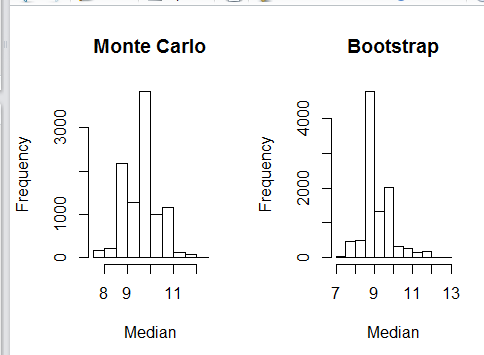
之后检验二者标准差,发现差别并不大:
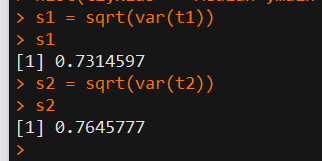
拔靴法--Bootstrap--R语言实现的更多相关文章
- 基于R语言的时间序列指数模型
时间序列: (或称动态数列)是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列.时间序列分析的主要目的是根据已有的历史数据对未来进行预测.(百度百科) 主要考虑的因素: 1.长期趋势(Lon ...
- R语言︱噪声数据处理、数据分组——分箱法(离散化、等级化)
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 分箱法在实际案例操作过程中较为常见,能够将一些 ...
- R语言︱缺失值处理之多重插补——mice包
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 笔者寄语:缺失值是数据清洗过程中非常重要的问题 ...
- 用R语言实现对不平衡数据的四种处理方法
https://www.weixin765.com/doc/gmlxlfqf.html 在对不平衡的分类数据集进行建模时,机器学**算法可能并不稳定,其预测结果甚至可能是有偏的,而预测精度此时也变得带 ...
- R语言中的机器学习包
R语言中的机器学习包 Machine Learning & Statistical Learning (机器学习 & 统计学习) 网址:http://cran.r-project ...
- R 语言实战-Part 3 笔记
R 语言实战(第二版) part 3 中级方法 -------------第8章 回归------------------ #概念:用一个或多个自变量(预测变量)来预测因变量(响应变量)的方法 #最常 ...
- 几种经典排序算法的R语言描述
1.数据准备 # 测试数组 vector = c(,,,,,,,,,,,,,,) vector ## [] 2.R语言内置排序函数 在R中和排序相关的函数主要有三个:sort(),rank(),ord ...
- R语言 常见模型
转自 雪晴网 [R]如何确定最适合数据集的机器学习算法 抽查(Spot checking)机器学习算法是指如何找出最适合于给定数据集的算法模型.本文中我将介绍八个常用于抽查的机器学习算法,文中还包括各 ...
- R语言学习笔记:向量
向量是R语言最基本的数据类型. 单个数值(标量)其实没有单独的数据类型,它只不过是只有一个元素的向量. x <- c(1, 2, 4, 9) x <- c(x[1:3], 88, x[4] ...
随机推荐
- 使用HttpClient发送数据 到WebApi
发送和JSON数据 /=============================webAPI接受POST的JOSN数据=============================/ POST api/& ...
- linux mysql导入导出
linux下导入.导出mysql数据库命令 一.导出数据库用mysqldump命令(注意mysql的安装路径,即此命令的路径):1.导出数据和表结构:mysqldump -u用户名 -p密码 数据库名 ...
- find函数
Python find() 方法检测字符串中是否包含子字符串 str ,如果指定 beg(开始) 和 end(结束) 范围,则检查是否包含在指定范围内,如果包含子字符串返回开始的索引值,否则返回-1. ...
- JAVA线程锁-读写锁应用,简单的缓存系统
在JAVA1.5版本以后,JAVA API中提供了ReadWriteLock,此类是一个接口,在它的实现类中ReentrantReadWriteLock中有这样一段代码 class CachedDat ...
- Mysql常用数据类型
Mysql常用数据类型 数字: 字符串: 时间:
- QT笔记之VS开发添加类
1. 2. 3.
- 使用GIt向github上传代码
github是一个基于git的代码托管平台,付费用户可以建私人仓库,我们一般的免费用户只能使用公共仓库,也就是代码要公开.这对于一般人来说公共仓库就已经足够了. 1.注册账户以及创建仓库 要想 ...
- LuaStudio 9.27 去10分钟退出暗桩板
http://bbs.pediy.com/showthread.php?p=1428203#post1428203
- Analyzer报表结果行
声明:原创作品,转载时请注明文章来自SAP师太技术博客( 博/客/园www.cnblogs.com):www.cnblogs.com/jiangzhengjun,并以超链接形式标明文章原始出处,否则将 ...
- Sprint(第六天11.19)
燃尽图
