bzoj 1911: [Apio2010]特别行动队 -- 斜率优化

1911: [Apio2010]特别行动队

Time Limit: 4 Sec  Memory Limit: 64 MB

Description

Input

Output

Sample Input

4
-1 10 -20
2 2 3 4

Sample Output

9

HINT

Source

dp方程：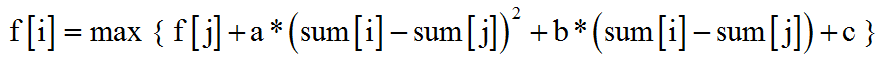

如果j>k且j比k更优

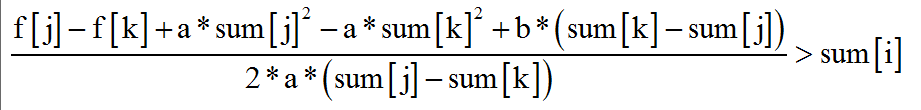
#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
#define N 1000100
#define db double
char xB[<<],*xS=xB,*xTT=xB;
#define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++)
#define isd(c) (c>='0'&&c<='9')
inline int read(){
    char xchh;
    int xaa;
    while(xchh=getc(),!isd(xchh));(xaa=xchh-'');
    while(xchh=getc(),isd(xchh))xaa=xaa*+xchh-'';return xaa;
}
int n,a,b,c,x[N],q[N],l,r,t;
ll f[N],sum[N];
inline ll sqr(ll x){return x*x;}
inline db cal(int j,int k){return (db)(f[j]+a*sqr(sum[j])-b*sum[j]-f[k]-a*sqr(sum[k])+b*sum[k])/(db)(*a*(sum[j]-sum[k]));}
int main()
{
    scanf("%d%d%d%d",&n,&a,&b,&c);
    for(int i=;i<=n;i++) x[i]=read();
    for(int i=;i<=n;i++) sum[i]=sum[i-]+x[i];
    for(int i=;i<=n;i++)
    {
        while(l<r&&cal(q[l],q[l+])<sum[i]) l++;
        t=q[l];
        f[i]=f[t]+a*sqr(sum[i]-sum[t])+b*(sum[i]-sum[t])+c;
        while(l<r&&cal(q[r-],q[r])>cal(q[r],i)) r--;
        q[++r]=i;
    }
    printf("%lld\n",f[n]);
    return ;
}