《用 Python 学微积分》笔记 3

《用 Python 学微积分》原文见参考资料 1。

16、优化

用一个给定边长 4 的正方形来折一个没有盖的纸盒，设纸盒的底部边长为 l，则纸盒的高为 (4-l)/2，那么纸盒的体积为：

$$V(l)=l^2\frac{4-l}{2}$$

怎样才能使纸盒的容积最大？也就是在 l>0,4-l>0 的限制条件下，函数 V(l) 的最大值是多少？

优化问题关心的就是这样的问题，在满足限制条件的前提下，怎么才能使目标函数最大（或最小）？

先来看下 V(l) 的函数图形：

import numpy as np
import matplotlib.pyplot as plt

l = np.linspace(0,4,100)
V = lambda l: 0.5*l**2*(4-l)
plt.plot(l,V(l))

plt.show()

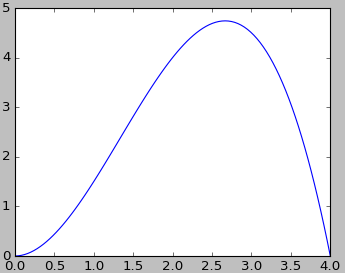
看得出来，V(l) 在大约 2.5 处最大。

如果给定一个函数，知道它在点 x=a 处的函数导数为 0，或者该点的导数不存在，则称该点为关键点。要想知道 f(a) 是局部最大值还是局部最小值，可以使用二次导数测试。

如果 f''(a)>0，则函数 f 在 a 处的函数值是局部最小值。

如果 f''(a)<0，则函数 f 在 a 处的函数值是局部最大值。

如果 f''(a)=0，则测试无法告诉我们结论。

上述二次导数测试可以从泰勒级数中推导出来。f(x) 在 x=a 处的泰勒级数为：

$$f(x)=f(a)+f'(a)(x-a)+\frac{1}{2}f''(a)(x-a)^2+\dots$$

因为 a 为关键点，f'(a)=0，所以：

$$f(x)=f(a)+\frac{1}{2}f''(a)(x-a)^2+O(x^3)$$

当 f''(a)≠0 时，f(x) 在 x=a 附近的表现近似于二次函数，二次项的系数 0.5f''(a) 决定了抛物线的开口朝向，因而决定了函数值在该点是怎样的。

回到之前求最大盒子体积的问题，解法如下：

import sympy
from sympy.abc import l
V = 0.5*l**2*(4-l)
# 看看一次导函数：
print V.diff(l)
# output is : -0.5*l**2 + 1.0*l*(-l + 4)
# 一次导函数的定义域为(-oo,oo),因此关键点为V'(l)=0的根
cp = sympy.solve(V.diff(l),l)
print cp
# output is: [0.0, 2.66666666666667]
# 找到关键点后，使用二次导数测试：
for p in cp:
    print V.diff(l,2).subs(l,p)
# output is: 4, -4
# 因此知道在l=2.666666处时，纸盒的体积最大

17、线性回归

二维平面上有 n 个数据点，p_i=(x_i,y_i)，现尝试找到一条经过原点的直线，y=ax，使得所有数据点到该直线的残差的平方和最小。

import numpy as np
import matplotlib.pyplot as plt

# 设定好随机函数种子，确保模拟数据的可重现性
np.random.seed(123)

# 随机生成一些带误差的数据
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res

# 求解回归线的系数
a = sum(x*y)/sum(x**2)

# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red')
for i in range(len(x)):
    plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\
         max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\
         color = 'black')

plt.show()

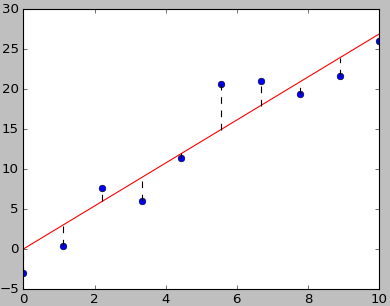
要找到这样一条直线，实际上是一个优化问题：

$$\underset{a}{min}Err(a)=\sum_{i}{(y_i-ax_i)}^2$$

要找出函数 Err(a) 的最小值，首先计算一次导函数：

$$\frac{dErr}{da}=\sum_{i}2(y_i-ax_i)(-x_i)$$

$$\qquad = -2\sum_{i}x_iy_i + 2a\sum_{i}x_i^2$$

令该函数为 0，求解出关键点：

$$a = \frac{\sum_{i}x_iy_i}{\sum_{i}x_i^2}$$

使用二次导数测试：

$$\frac{d^2Err}{da^2}=2\sum_ix_i^2>0$$

因此

$$a = \frac{\sum_{i}x_iy_i}{\sum_{i}x_i^2}$$

是能够使函数值最小。这也是上面 Python 代码中，求解回归线斜率所用的计算公式。

如果不限定直线一定经过原点，即公式为 y=ax+b，则同样还是一个优化问题，只不过涉及的变量变成两个。

$$\underset{a}{min}Err(a,b)=\sum_i{(y_i-ax_i-b)}^2$$

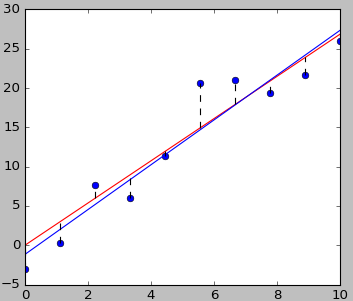
这个问题是多元微积分里要分析的问题，这里先给出 Python 中的求解方法。红线为经过原点的直线，蓝线为不限定经过原点的直线。

import numpy as np
import matplotlib.pyplot as plt

# 设定好随机函数种子，确保模拟数据的可重现性
np.random.seed(123)

# 随机生成一些带误差的数据
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res

# 求解回归线的系数
a = sum(x*y)/sum(x**2)

slope, intercept = np.polyfit(x,y,1)

# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red')
plt.plot(x,slope*x+intercept, 'blue')
for i in range(len(x)):
    plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\
         max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\
         color = 'black')

plt.show()

18、不定积分

根据加速度 a(t) 求速度 v(t)，可得：

$$\frac{dv}{dt}=a(t)$$

一旦找到了 v(t)，那么

$$\forall C\in\mathbb{R}, v(t)+C$$

也都是方程的解，因此常微分方程的解是 v(t)+C 这样一系列函数。得出这一系列函数后，只需知道任一时刻汽车的速度，便可求出常数项 C。

Python 中积分的方法：

import sympy

t = sympy.Symbol('t')
v = t**3-3*t-6
a = v.diff()
print a.integrate()
# result is : t**3 - 3*t
print sympy.integrate(sympy.E**t+3*t**2)
# result is : t**3 + exp(t)

参考资料：

[1] https://ryancheunggit.gitbooks.io/calculus-with-python/content/