CodeForces - 963B Destruction of a Tree （dfs+思维题）

B. Destruction of a Tree

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a tree (a graph with n vertices and n - 1 edges in which it's possible to reach any vertex from any other vertex using only its edges).

A vertex can be destroyed if this vertex has even degree. If you destroy a vertex, all edges connected to it are also deleted.

Destroy all vertices in the given tree or determine that it is impossible.

Input

The first line contains integer n (1 ≤ n ≤ 2·105) — number of vertices in a tree.

The second line contains n integers p1, p2, ..., pn (0 ≤ pi ≤ n). If pi ≠ 0 there is an edge between vertices i and pi. It is guaranteed that the given graph is a tree.

Output

If it's possible to destroy all vertices, print "YES" (without quotes), otherwise print "NO" (without quotes).

If it's possible to destroy all vertices, in the next n lines print the indices of the vertices in order you destroy them. If there are multiple correct answers, print any.

Examples

input

Copy

5
0 1 2 1 2

output

Copy

YES
1
2
3
5
4

input

Copy

4
0 1 2 3

output

Copy

NO

Note

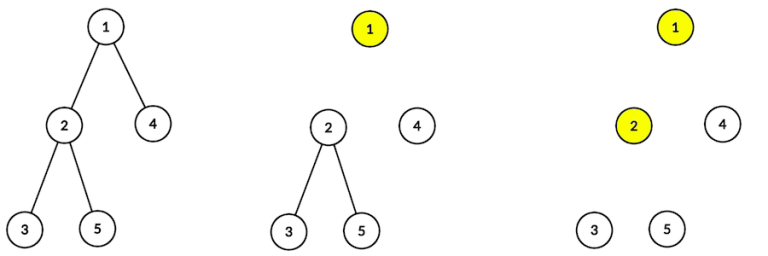
In the first example at first you have to remove the vertex with index 1 (after that, the edges (1, 2) and (1, 4) are removed), then the vertex with index 2 (and edges (2, 3) and (2, 5) are removed). After that there are no edges in the tree, so you can remove remaining vertices in any order.

题目大意：给你一棵树，只能删除度数为偶数的节点，节点删除后，与它相连的边也会删除。问你能否把所有点删除。

解题思路：只要你能想到，如果一棵树，有偶数条边，那么他一定能被删除完！或者说，一棵树有奇数个节点，那么他肯定能被删除完！因为，如果边为奇数，每次删除偶数条边，最后肯定剩奇数个边啊！如果边为偶数，每次删除偶数条边，最后肯定能删除完！所以基于这个思想，我们递归的删除点即可。从根节点开始，如果某一棵子树他的节点个数为偶数（加上当前节点就为奇数了），那么就深搜这颗子树，递归删除。

#include <bits/stdc++.h>
using namespace std;  

vector<int> ch[];
int sz[];  

void getsize(int u, int pre)
{
    sz[u] = ;
    for (int i = ; i < ch[u].size(); ++i)
    {
        if (ch[u][i] != pre)
        {
            getsize(ch[u][i], u);
            sz[u] += sz[ch[u][i]];
        }
    }
}  

void dfs(int u, int pre)
{
    for (int i = ; i < ch[u].size(); i++)
    {
        if (ch[u][i] != pre)
        {
            if (sz[ch[u][i]] %  == )
            {
                dfs(ch[u][i], u);
            }
        }
    }  

    printf("%d\n", u);  

    for (int i = ; i < ch[u].size(); i++)
    {
        if (ch[u][i] != pre)
        {
            if (sz[ch[u][i]] %  == )
            {
                dfs(ch[u][i], u);
            }
        }
    }
}  

int main()
{  

    int N;
    scanf("%d", &N);
    int temp;
    int root;
    for (int i = ; i <= N; i++)
    {
        scanf("%d", &temp);
        if (temp != )
        {
            ch[i].push_back(temp);
            ch[temp].push_back(i);
        }
        else
        {
            root = i;
        }
    }  

    if (N %  == )
    {
        printf("NO\n");
    }
    else
    {
        getsize(root,-);
        printf("YES\n");
        dfs(root, -);
    }  

    return ;
}  

我wa的代码，原因是，我的写法是每次找出边是偶数的，删掉，再继续，仔细思考找到了可以把我wa的样例：

先删1的话，会导致输出“NO”

#include <iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<deque>
#include<vector>
#include<queue>
#define ll unsigned long long
#define inf 0x3f3f3f3f
using namespace std;
vector<int>v[];
bool us[];
int in[];
queue<int>q;
int main()
{
    int n;
    cin>>n;
    memset(us,,sizeof(us));
    memset(in,,sizeof(in));
    while(!q.empty()) q.pop();
    for(int i=;i<=n;i++)
    {
        int x;
        cin>>x;
        if(x!=)
        {
            v[x].push_back (i);
            v[i].push_back (x);
            in[i]++;
            in[x]++;
        }
    }
    if(n%==) cout<<"NO"<<endl;
    else
    {
        while()
        {
            int k=-;
            for(int i=;i<=n;i++)
            {
                if(!us[i]&&in[i]%==)
                {
                    k=i;
                    break;
                }
            }
            if(k==-) break;
            q.push(k);
            us[k]=;
            for(int j=;j<v[k].size ();j++)
            {
                int y=v[k][j];
                if(us[y]) continue;
                in[y]--;
            }
        }
        bool f=;
        for(int i=;i<=n;i++)
        {
            if(!us[i])
            {
                f=;
                break;
            }
        }
        if(!f) cout<<"NO";
        else
        {
            cout<<"YES"<<endl;
            while(!q.empty ())
            {
                cout<<q.front()<<endl;
                q.pop();
            }
        }
    }
    return ;
}