Codeforces-591C题解

一、题目链接

　　http://codeforces.com/problemset/problem/591/C

二、题意

　　给定一个只含数字0和1的数组，通过如下方式，变成不再变化的01组合，最少需要操作几次。并输出最后得到的“稳定”01串。

　　操作方式：数组开头和结尾两个数不变，对于不是开头和结尾的数字a[i]，a[i] = (a[i - 1], a[i], a[i + 1])三个数的中位数。

　　比如：1 0 1 0 1 0 1

　　一次：1 1 0 1 0 1 1

　　两次：1 1 1 1 1 1 1

　　输出：2

　　　　　1 1 1 1 1 1 1

三、思路

　　1、这题纯属找规律题，对于连续一排（两个及以上）的0或1，无论怎么变，都和原来一样。

　　2、对于101010......这种组合：

　　　　（1）如果长度为奇数，则通过若干次操作后可使这一段变为和开头元素一样。即开头和结尾是0，则通过若干次操作后这段序列变成000……000，如果开头和结尾是1，则通过若干次操作后这段序列变成111……111。

　　　　（2）如果长度为偶数，如果头是0、尾是1，则通过若干次操作后这段变成前一半是0，后一半是1；如果头是1、尾是0，则通过若干次操作后这段变成前一半是1，后一半是0。

　　3、对于操作次数的问题，可以打表找到规律如下。

　　　　

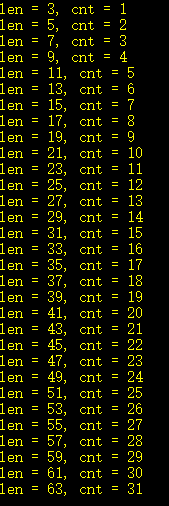
　　4、可以发现，当长度为2n + 1时（头尾是0和头尾是1是一样的），需要操作的次数为n。同理，当长度为2n时（头尾为0……1和头尾为1……0是一样的），需要操作的次数为n - 1。

　　5、找到规律后，遍历一次数字串，记录满足01交叉的子串的起始和末尾下标。然后遍历所有满足01交叉的子串，使用上述规律，记录操作次数的最大值即为结果的第一部分。同时，对该子串使用上述规律做替换，然后输出整个序列即可。

四、正确性证明

　　如果某段a[i], a[i + 1], ……，a[j]子串满足01交叉，len = j - i + 1：

　　1、如果len为奇数，不妨假设为1010……101，则a[i - 1]和a[j + 1]必为1（不然还可以更长），因为串头和串尾是不变的，而且每操作一次，最靠近开头和结尾的0就会变成1，所以，这段子串必然要经过上述的规律次数才能变成“稳定”串（因为没人可以帮它，它也不能帮别人）。所以上述找规律的操作对于每一段满足01交叉的子串都是独立的，不会相互影响。同理，0101……010这样的子串道理也是一样的。

　　2、如果len为偶数，不妨假设为1010……10，则a[i - 1]必为1，a[j + 1]必为0（不然还可以更长），然后证明过程和上述一样了。

五、源代码

　　

#include<bits/stdc++.h>
using namespace std;
int n;
];

typedef pair<int, int> PII;
vector<PII> vec;
int main() {
#ifndef ONLINE_JUDGE
    freopen("input.txt", "r", stdin);
#endif // ONLINE_JUDGE
    int s, t;
    while(~scanf("%d", &n)) {
        vec.clear();
        ; i <= n; ++i)scanf("%d", a + i);
        ; i <= n; ++i) {
            ]) {
                ; i <= n && a[i] ^ a[i - ]; ++i);
                t = i;
                vec.push_back(make_pair(s, t));
            }
        }
        ;
        , sz = vec.size(); i < sz; ++i) {
            PII& p = vec[i];
            int len = p.second - p.first;
             == ) {
                ans = max(ans, (len - ) / );//len为奇数，len / 2 == (len - 1) / 2。
                for(int k = p.first; k < p.second; ++k)a[k] = a[p.first];
            } else {
                ans = max(ans, (len - ) / );
                ; ++k)a[k] = a[p.first];
                ; k < p.second; ++k)a[k] = a[p.second - ];
            }
        }
        printf("%d\n", ans);
        ;i <= n;++i)printf("%d%c", a[i], i < n ? ' ' : '\n');
    }
    ;
}

六、附：找规律程序源代码（注意体会二进制的思想）

#include<bits/stdc++.h>
using namespace std;

int bit(long long& a, int x) {
    ;
}

int main() {
    ; i <= ; i += ) {
        , b = ;
        ; j < i; j += )a |= 1LL << j;
        ;
         && a != (1LL << i) - ) {
            b = a;
            ; j < i - ; ++j) {
                ) == bit(a, j + ) && bit(a, j - ) == )b |= (1LL << j);
                ) == bit(a, j + ) && bit(a, j - ) == )b &= ~(1LL << j);
            }
            a = b;
            ++cnt;
        }
        printf("len = %d, cnt = %d\n", i, cnt);
    }
    ;
}