C#数据结构-二叉树-顺序存储结构

什么是二叉树：每个树的节点只有两个子树的树形结构。

为什么使用顺序存储结构：使用数组存放满二叉树的各结点非常方便，可以根据一个结点的索引号很容易地推算出它的双亲、孩子、兄弟等结点的编号，从而对这些结点进行访问，这是一种存储二叉满二叉树或完全二叉树的最简单、最省空间的做法。

 /// <summary>
/// 顺序存储二叉树
/// </summary>
public class SequentialStorageBinaryTree<T>
{
    /// <summary>
    /// 用于存储节点的数组
    /// </summary>
    private T[] data;
    /// <summary>
    /// 节点数
    /// </summary>
    private int count;

    public SequentialStorageBinaryTree(T[] arr = null)
    {
        if (arr == null)
            data = new T[0];
        else
            data = arr;
        count = data.Length;
    }

    /// <summary>
    /// 增加
    /// </summary>
    /// <param name="item"></param>
    public bool Add(T item)
    {
        List<T> list = data.ToList<T>();
        list.Add(item);
        data = list.ToArray();
        count = data.Length;
        return true;
    }
}

通过数组存储结构为：

1、层次遍历

/// <summary>
/// 层次遍历
/// </summary>
public void LevelTraversal()
{
    for (int i = 0; i < count; i++)
    {
        Console.Write(data[i] + " ");
    }
}

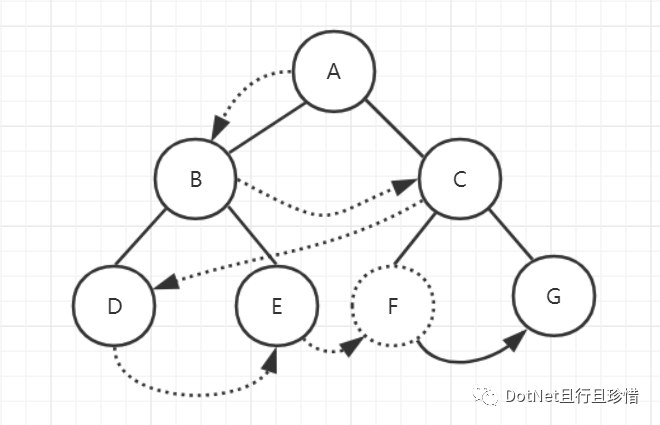
2、先序遍历

/// <summary>
/// 先序遍历
/// </summary>
/// <param name="index"></param>
public void PreorderTraversal(int index =0)
{
    //递归的终止条件
    if (index >= count || index <0)
        return;
    int number = index + 1;
    Console.Write(data[index] + " ");
    int leftIndex = number * 2;//做节点
    int rightIndex = number * 2 + 1;
    PreorderTraversal(leftIndex - 1);
    PreorderTraversal(rightIndex - 1);
}

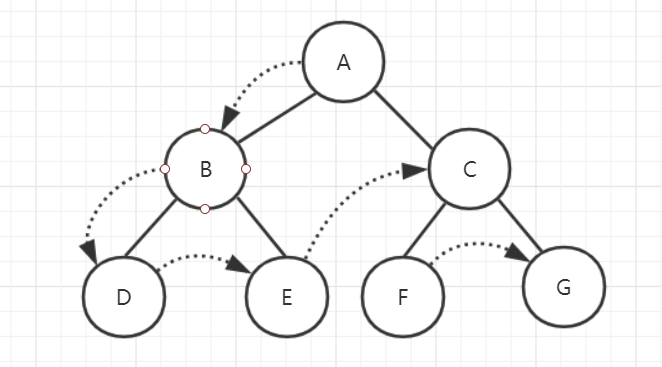
3、中序遍历

/// <summary>
/// 中序遍历
/// </summary>
/// <param name="index"></param>
public void MiddlePrefaceTraversal(int index = 0)
{
    //递归的终止条件
    if (index >= count || index < 0)
        return;
    int number = index + 1;

    int leftIndex = number * 2;//做节点
    int rightIndex = number * 2 + 1;
    MiddlePrefaceTraversal(leftIndex - 1);
    Console.Write(data[index] + " ");
    MiddlePrefaceTraversal(rightIndex - 1);
}

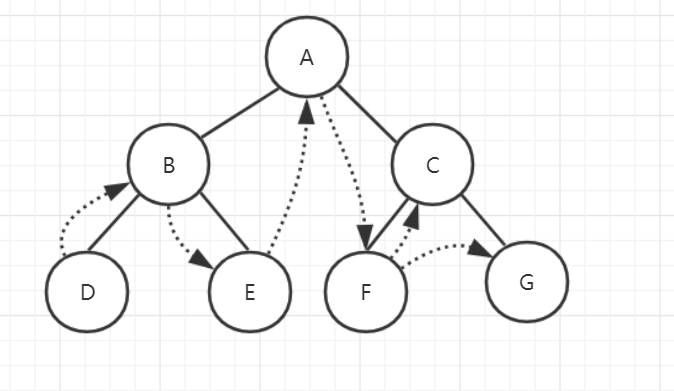
4、后续遍历

/// <summary>
/// 后序遍历
/// </summary>
/// <param name="index"></param>
public void AfterwordTraversal(int index = 0)
{
    //递归的终止条件
    if (index >= count || index < 0)
        return;
    int number = index + 1;
    int leftIndex = number * 2;//做节点
    int rightIndex = number * 2 + 1;
    AfterwordTraversal(leftIndex - 1);
    AfterwordTraversal(rightIndex - 1);
    Console.Write(data[index] + " ");
}

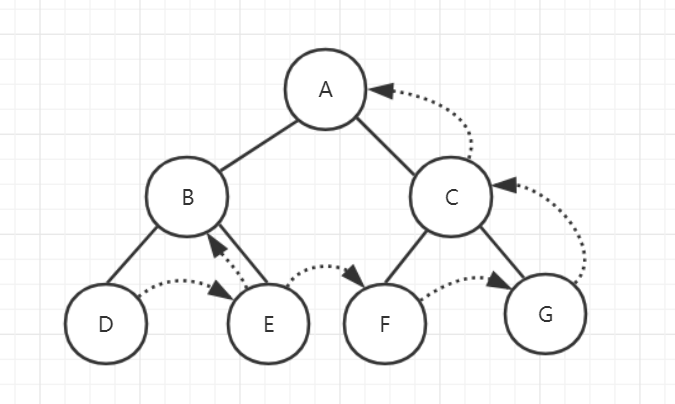
现在我们测试下：

SequentialStorageBinaryTree<string> bTree = new SequentialStorageBinaryTree<string>();
bTree.Add("A");
bTree.Add("B");
bTree.Add("C");
bTree.Add("D");
bTree.Add("E");
bTree.Add("F");
bTree.Add("G");

//先序遍历
Console.Write("先序遍历：");
bTree.PreorderTraversal();
Console.WriteLine();

//中序遍历
Console.Write("中序遍历：");
bTree.MiddlePrefaceTraversal();
Console.WriteLine();

//中序遍历
Console.Write("后序遍历：");
bTree.AfterwordTraversal();
Console.WriteLine();

//层次遍历
Console.Write("层次遍历：");
bTree.LevelTraversal();
Console.ReadKey();

输出：

---