Java数据结构——树、二叉树的理论知识汇总

通用树的理论知识

一、树的定义

由一个或多个（n>=0）节点组成的有限集合T，有且仅有一个节点称为根（root），当n>1时，其7余的节点为m（m>=0）个互不相交的有限集合T1，T2，...，Tm。每个集合本身又是棵树，称其为根的子树。
注意：空树也是树，树具有递归性。

二、树的相关术语
1. 根：根节点（没有前驱）。
2. 叶子：终端节点（没有后继）。
3. 森林：m棵不相交树的集合。
4. 有序树：节点从上至下、从左至右有有序，不能互换
5. 双亲：节点的直接前驱。
6. 孩子：节点的直接后继。
7. 兄弟：同一双亲下的同层节点。
8. 堂兄弟：不同双亲的同层节点。
9. 祖先：从根节点到该节点所经分支的所有节点。
10. 子孙：从该节点的下层子树的任一节点。
11. 节点：树的数据元素。
12. 节点的度：直接后继的个数。
13. 节点的层次：从根到该节点的层数，根节点所在的层数为1。
14. 终端节点：度数为0的节点，就是叶子。
15. 分支节点：树根除外的节点。
16. 树的度：所有节点度中的最大值。
17. 树的深度：所有节点中最大的层数。

三、树的表示法
1. 广义表示法：（A（B（E（K，L），F）,C（G），D（H（M），I，J）））
2. 左孩子右兄弟表示法:每个节点有两个指针域，一个指向其长子，另一个指向其兄弟。
3.双亲表示法:让每个结点记住其父结点的位置。存储数据元素的结点由两部分组成：存储数据元素值的数据字段，以及存储父结点位置的字段。

四、树的物理存储结构

顺序储存、链式存储。

五、树的运算

普通的树如果不能转化为二叉树，则运算很难实现。二叉树的运算有插入、删除、修改、查找、排序等，这些操作必须建立在对树节点遍历之上。

六、普通树转二叉树（左儿子，右兄弟）

1. 将树的根节点直接作为二叉树的根节点。
2. 将树的根节点的第一个子节点作为根节点的左儿子，若该子节点存在兄弟节点，则将该子节点的第一个兄弟节点（方向从左往右）作为该子节点的右儿子。
3. 将树中的剩余节点按照上一步的方式，依序添加到二叉树中，直到树中所有的节点都在二叉树中。

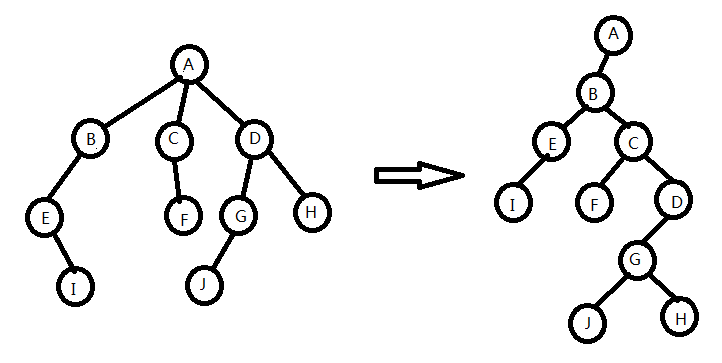
其实就是每个点的左儿子是它的第一个儿子，右儿子是它从左往右数的第一个兄弟。

二叉树的补充理论知识

一、二叉树的定义

n（n>=0）个节点的有限集合，由一个根节点以及两棵互不相交的左子树、右子树组成。

二、二叉树逻辑结构

一对二（1:2）

三、二叉树基本特征

每个节点最多只有两棵子树，不存在度大于2的节点，左子树和右子树次序不能颠倒。

四、二叉树的五种基本形态
（1）空二叉树；

（2）只有一个根结点；

（3）根结点只有左子树；

（4）根结点只有右子树（完全二叉树不具备这种形态）；

（5）根结点既有左子树又有右子树。

五、二叉树的性质
1. 二叉树的第i层上至多有2的i-1次方个节点（i>0）。
2. 深度为k的二叉树至多有2的k次方-1个节点（k>0）。
3. 二叉树，n0 = n2 + 1（n0表示叶子数，n2表示度为2的节点数）
4. 满二叉树：每层都充满了节点
5. 完全二叉树：满二叉树中，编号1~n，满足至上而下、从左至右与节点一一对应。完全二叉树最后一层叶子可以不满，但必须集中在左边。
6. 完全二叉树，具有n个节点的深度必为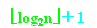

7. 完全二叉树，若编号为i的节点，其左孩子编号必为2i，其右孩子编号必为2i+1。
8.满二叉树的特点：
（1）叶子只能出现在最下一层。出现在其他层就不可能达到平衡。
（2）非叶子结点的度一定是2。
（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。
9.完全二叉树的特点：
（1）叶子结点只能出现在最下两层。
（2）最下层的叶子一定集中在左部连续位置
（3）倒数二层，若有叶子结点，一定都在右部连续位置。
（4）如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。
（5）同样结点数的二叉树，完全二叉树的深度最小。
注意：满二叉树一定是棵完全二叉树，但完全二叉树不一定是满的。
10.题目：深度为9的二叉树中至少有多少个节点，答：9个节点（注意:这里是二叉树而不是完全二叉树）
11.为什么要研究满二叉树和完全二叉树这两种特殊形式，答：只有这两种形式可以实现顺序存储。
12.完全二叉树，具有1000个节点，则叶子节点有多少个，度为2的节点有多少个，有多少个节点只有非空左子树，有多少个节点只有非空右子树。答：总层数：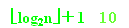

，完全二叉树前9层总节点数为511个，末层叶子数为489个，叶子数为奇数说明有一个非空左子树，完全二叉树不可能出现只有右子树
13.树执行查找、删除、插入的时间复杂度都是O(logN)

五、二叉树的顺序存储

按二叉树的节点“自上而下，从左至右”编号，用一组连续的存储单元存储。
规律：下标为i的双亲，其左孩子下标必定为2i，其右孩子下标必定为2i+1，例如[2]、[4]、[5]
若不是完全二叉树就转化为完全二叉树，方法简单，就是将各层空缺统统补上节点，内容为空，缺点：浪费空间，插入删除不方便。

六、二叉树的链式存储结构

用二叉链表即可方便表示，从根节点开始存储，相应的，访问树中的节点也只能从根节点开始。
如果需要倒插某节点的双亲，可以再增加一个双亲域（直接前趋）指针，将二叉链表变成三叉链表。

七、遍历二叉树
1. 遍历又称周游。
2. 遍历的用途：是树结构插入、删除、修改、查找、排序运算的前提。
3. 遍历方法：先左后右

八、遍历方案（下一篇博文会具体实现树的遍历）

先（根）序遍历，中（根）序遍历、后（根）序遍历，层序遍历。