[Fundamental of Power Electronics]-PART II-9. 控制器设计-9.3 关键项1/(1+T)和T/(1+T)以及闭环传递函数的构建

9.3 关键项\(1/(1+T)\)和\(T/(1+T)\)以及闭环传递函数的构建

从式(9.4)到(9.9)的传递函数可以很容易的由图形代数方法进行构建。假设我们已经分析了反馈系统模块，并且已经画出了\(||T(s)||\)的bode图。举一个具体的例子，假设结果为图9.5所示，其中\(T(s)\)为：

\[T(s)=T_{0} \cfrac{(1+\cfrac{s}{\omega_{z}})}{(1+\cfrac{s}{Q\omega_{p1}}+(\cfrac{s}{\omega_{p1}})^2)(1+\cfrac{s}{\omega_{p2}})} \tag{9.10}
\]

这个例子看起来有一点复杂，但实际的稳压器的环路增益通常甚至更加复杂，并且可能包含四个，五个甚至更多的极点。分析(9.5)到(9.7)，要确定闭环传递函数，需要进行大量工作。环路增益必须要加1，并且重构所得的分子和分母。使用这种方法，很难获得对闭环传递函数和环路增益之间关系的物理本质了解。这样的结果就是，难以设计满足规格的反馈回路。

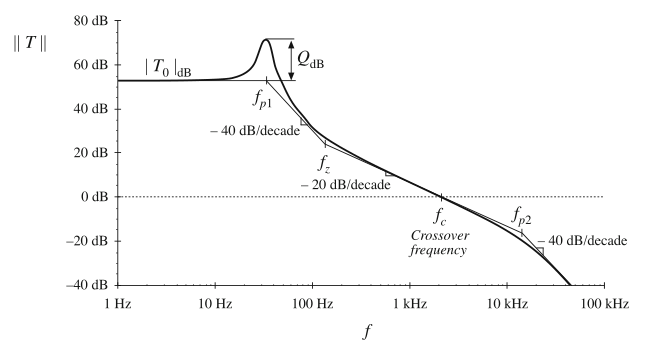
Fig. 9.5 Magnitude of the loop gain example, Eq. (9.10)

利用图形代数方法，闭环传递函数可以通过观察的方式构建，并且这些传递函数与环路增益的关系也变得显而易见了。让我们首先来研究如何画出\(||T/(1+T)||\)。从图9.5可以看到，存在被称为穿越频率(crossover frequency)的\(f_{c}\)，使得\(||T||=1\)。在频率小于\(f_{c}\)时，\(||T||>1\)；事实上，对于\(f<<f_{c}\)时，\(||T||>>1\)。因此，在低频处，\((1+T) \approx T\)，并且\(T/(1+T) \approx T/T=1\)。在频率大于\(f_{c}\)处，\(||T||<1\)，并且当\(f>>f_{c}\)时\(||T||<<1\)。因此，在高频处，\((1+T) \approx 1\)并且\(T/(1+T)\approx T/1=T\)。因此我们得到：

\[\cfrac{T}{1+T} \approx
\begin{cases}
1\ for\ ||T||>>1 \\
T\ for\ ||T||<<1
\end{cases} \tag{9.11}
\]

对应于式(9.11)的渐近线相对的就比较容易构建了。当\(f<f_{c}\)时，低频渐近线为1或者0 dB。\(f>f_{c}\)的高频渐近线为T。结果如图9.6所示。

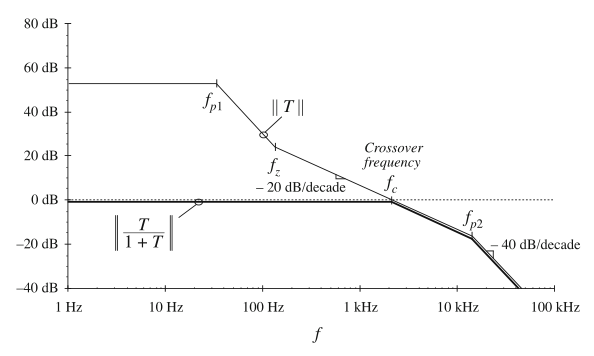
Fig. 9.6 Graphical construction of the asymptotes of \(||T/(1 + T)||\). Exact curves are omitted

因此，在低频段，\(||T||\)比较大，给定-输出传递函数为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{ref}(s)}=\cfrac{1}{H(s)} \cfrac{T(s)}{1+T(s)} \approx \cfrac{1}{H(s)} \tag{9.12}
\]

这是一个期望的特性，并且反馈环路在\(||T||\)比较大的频率下都能很好的工作。在高频段(\(f>>f_{c}\))，其中\(||T||\)很小，那么给定-输出传递函数为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{ref}(s)}=\cfrac{1}{H(s)} \cfrac{T(s)}{1+T(s)} \approx \cfrac{T(s)}{H(s)}=\cfrac{G_{c}(s)G_{vd}(s)}{V_{M}} \tag{9.13}
\]

这并不是我们期望的特性，实际上，这是将反馈回路断开的增益(\(H \rightarrow 0\))。在高频段，由于\(T\)的带宽有限，因此反馈回路无法消除干扰。通过将图9.6中的\(T/(1+T)\)的渐近线乘以\(1/H\)，就可以在图形上构建出给定-输出传递函数。

因此，穿越频率(crossover frequency)\(f_{c}\)代表了反馈系统的带宽，并且在该带宽内，闭环特性得以改善。进一步地，可以从图9.6中看出反馈使系统\(T\)的极点移动了：\(T\)在\(f_{p1}\)处包含两个极点，但\(T/(1+T)\)中并不存在，而\(T/(1+T)\)在\(f_{c}\)处包含一个极点。可以看出的是，\(T\)的一个极点从频率\(f_{p1}\)大致移动到了\(f_{z}\)，这样二者抵消了。\(f_{p1}\)处的第二个极点从移动到了大约\(f_{c}\)处。图9.6表明了如何在反馈环路的带宽内增加极点的频率并改变其\(Q\)系数。

我们可以用同样的方式画出\(||1/(1+T)||\)的渐近线。在低频段，\(||T||>>1\)，那么\((1+T) \approx T\)，因此\(1/(1+T) \approx 1/T\)。在高频段，\(||T||<<1\)，那么\((1+T) \approx 1\)并且\(1/(1+T) \approx 1\)。因此我们有：

\[\cfrac{1}{1+T(s)} \approx
\begin{cases}
\cfrac{1}{T(s)}\ for\ ||T||>>1 \\
1\ \ \ \ for\ ||T||<<1
\end{cases} \tag{9.14}
\]

以图9.5中的\(T(s)\)为例的渐近线在图9.7中给出。

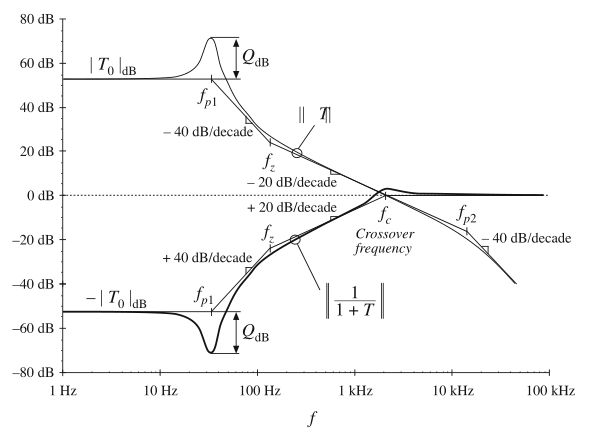
Fig. 9.7 Graphical construction of \(||1/(1 + T)||\)

在\(||T||\)很大的低频段，从\(v_{g}\)到\(v\)的扰动传递函数为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{g}(s)}=\cfrac{G_{vg}(s)}{1+T(s)} \approx \cfrac{G_{vg}(s)}{T(s)} \tag{9.15}
\]

同样的，\(G_{vg}(s)\)是不含反馈的原始传递函数。闭环传递函数幅值减小了系数\(1/||T||\)。因此，例如，如果我们想在120Hz，将传递函数缩小20倍，因此我们需要\(||T||\)在120Hz至少为\(20 \Rightarrow 26\ dB\)。通过将图9.7的渐近线乘以\(G_{vg}(s)\)的渐近线，可以在图形中构建\(v_{g}\)到\(v\)的传递函数。

类似的方法可以用于输出阻抗上。低频下的闭环输出阻抗为：

\[\cfrac{\hat{v}(s)}{-\hat{i}_{load}(s)}=\cfrac{Z_{out}(s)}{1+T(s)} \approx \cfrac{Z_{out}(s)}{T(s)} \tag{9.16}
\]

在小于穿越频率的频率段，输出阻抗的幅值在幅值上也减小系数为\(1/||T||\)。

在高频段\((f>f_{c})\)处，\(||T||\)很小，那么\(1/(1+T) \approx 1\)，并且：

\[\begin{aligned}
& \cfrac{\hat{v}(s)}{\hat{v}_{g}(s)}=\cfrac{G_{vg}(s)}{1+T(s)} \approx G_{vg}(s) \\
& \cfrac{\hat{v}(s)}{-\hat{i}_{load}(s)}=\cfrac{Z_{out}(s)}{1+T(s)} \approx Z_{out}(s)
\end{aligned} \tag{9.17}
\]

这与原始扰动传递函数和输出阻抗相同。因此，在高于穿越频率的频率段，反馈环路对扰动传递函数几乎没有影响。

图9.8a给出了一个具有由下式给出的环路增益\(T(s)\)的buck变换器的实例：

\[T(s)=H(s)G_{vd}(s)/V_{M} \tag{9.18}
\]

这个简单的示例没有包含补偿器。Buck变换器的LC滤波器在\(f=f_{p1}\)引入了谐振极点，并且电容等效串联电阻\(R_{C}\)在频率\(f_{z}\)处引入了一个极点。反馈传感器模块\(H(s)\)在\(f=f_{p2}\)处包含一个高频极点。因此，这个示例包含的环路增益\(T(s)\)与(9.10)相同。让我们假设我们的元件值选择使得其幅值如图9.5。因此，\(||1/(1+T)||\)在图9.7中给出了。

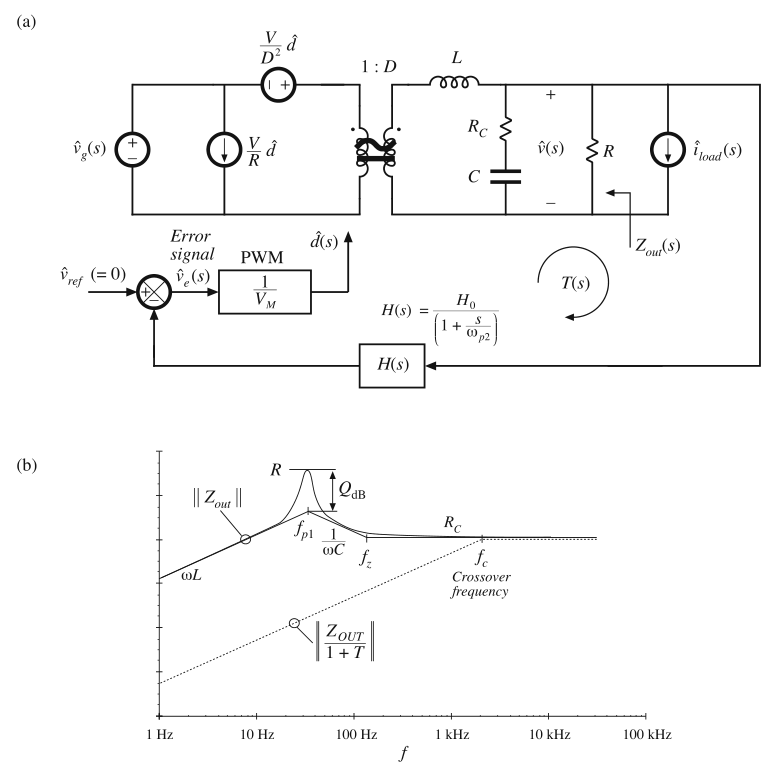
Fig. 9.8 Construction of the closed-loop output impedance of a simple buck regulator: (a) feedback

system, (b) open-loop (solid line) and closed-loop (dashed line) output impedance asymptotes

我们可以通过在图9.8a中将\(\hat{v}_{g}\)和\(\hat{d}\)设置为0，从而求解输出端口的阻抗，然后求解开环输出阻抗\(Z_{out}\)的bode图，其结果为：

\[Z_{out}(s)=sL//R//(R_{C}+\cfrac{1}{sC}) \tag{9.19}
\]

对于\(R_{C}<<R\)的典型情况，开环输出阻抗的近似bode图在图9.8b中进行了构建。接下来，通过将图9.8b所示的开环输出阻抗乘以图9.7所示的\(||1/(1+T)||\)的渐近线来构成闭环输出阻抗。在大于穿越频率\(f_{c}\)的频率段，输出阻抗将不受反馈回路的影响。在刚好低于\(f_{c}\)的频率处，反馈环路减小了输出阻抗，并且\(||1/(1+T)||\)项为\(||Z_{out}/(1+T)||\)引入了\(+20\ dB\)每十倍频程的斜率。在\(f=f_{z}\)处，\(Z_{out}\)的零点被\(1/(1+T)\)的极点对消了，因此，在闭环传递函数中没有观察到斜率的变化。同样的，在\(f=f_{p1}\)处，\(Z_{out}\)的谐振极点被\(1/(1+T)\)的谐振零点对消了。那么对于\(||Z_{out}/(1+T)||\)的斜率来说，仍然没有什么变化。这些对消的发生时因为功率级电路将同样的极点引入了\(G_{vd}(s)\)和\(Z_{out}(s)\)中了。

本章后面将给出另外一个示例，其中反馈的补偿器电路将不存在于\(Z_{out}(s)\)的零极点引入了\(T(s)\)。结果闭环输出阻抗表现了由补偿器动态引入\(||1/(1+T)||\)的零极点特性。