算法实验5--N皇后

实验名称

回溯法解N皇后问题

实验目的

掌握回溯递归算法、迭代算法的设计与实现；
设计回溯算法求解；
分析算法的时间复杂度。

实验环境

操作系统：win 10;

编程语言：Java；

开发工具：IDEA；

问题描述

在n×n格的国际象棋上摆放n个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法？

实验过程

回溯法

按照优先级条件向前搜索以达到目标。但是当探索到某一步时，发现原先选择并不能达到目标，就退回上一步重新选择，这种走不通就退回的技术叫做回溯。

问题解决思路

用数组模拟棋盘，从第一行开始，依次选择位置，如果当前位置满足条件，则向下选择位置，如果不满足条件，那么当前位置向后移动一位。

最后一个不满足，回溯到上一行，选择下一个位置继续进行探索。

其实并不需要一个n*n的数组，我们只需要一个长度为n的数组来存储位置，array[i] = k；表示第i行，第k个位置放皇后。

解题步骤

1．因为皇后之间不能放在同一行，同一列，同一斜线。所以每行放一个皇后，就解决了不在同一行的问题。result[row]=j；表示第row行，第j列放置皇后。

2．在第i行的时候，遍历n列，试探位置，和之前所有行放的位置进行比较。

3．判断当前位置是否可以放皇后：如果当前列和之前皇后所在的列相等即result[i] == col 或者在同一个斜线上： result[i] == col - sub || result[i] == col + sub；代表当前位置不合法，返回false，如果当前位置可以放置皇后，那就将这个位置的坐标记录下来result[row] = j;j代表的是皇后所在的列；

4．回溯，然后在下一行寻找皇后放置的位置。

代码实现

1.	package org.qianyan.algorithm;

2.

3.	import java.util.ArrayList;

4.	import java.util.Arrays;

5.	import java.util.List;

6.

7.	/**

8.	 * @Author Huhuitao

9.	 * @Date 2020/12/17 15:51

10.	 */

11.	public class NQueens {

12.	    public static void main(String[] args) {

13.	        NQueens nQueens = new NQueens();

14.	        long begin_time = System.currentTimeMillis();

15.	        int N = 8;

16.	        List<List<String>> lists = nQueens.solveNQueens(N);

17.	        long end_time = System.currentTimeMillis();

18.	        System.out.println(end_time - begin_time + "ms");

19.	        lists.stream().forEach(list -> {

20.	            System.out.println("==========================");

21.	            for (int i = 0; i < list.size(); i++) {

22.	                System.out.println(list.get(i));

23.	            }

24.	        });

25.	        System.out.println("==========================");

26.	        System.out.println(N+"皇后，有"+lists.size()+"种解决方案");

27.	    }

28.

29.	    private List<List<String>> results = new ArrayList<>(); // 结果集

30.

31.	    public List<List<String>> solveNQueens(int n) {

32.	        int[] result = new int[n]; // 记录每一行皇后放置的 列坐标

33.	        backtracking(result, 0);

34.	        return results;

35.	    }

36.

37.	    /**

38.	     * 回溯

39.	     *

40.	     * @param result

41.	     * @param row

42.	     */

43.	    private void backtracking(int[] result, int row) {

44.	        if (row == result.length) {

45.	            //递归结束条件，放置完成最后一行,将结果添加到results

46.	            List<String> temp = new ArrayList<>();

47.	            for (int i = 0; i < result.length; i++) {

48.	                char[] str = new char[row];

49.	                Arrays.fill(str, '.');

50.	                str[result[i]] = 'Q';

51.	                temp.add(new String(str)); // 根据每一行出现皇后的位置填充解

52.	            }

53.	            results.add(temp); // 加入当前解

54.

55.	        }

56.	        for (int j = 0; j < result.length; j++) {

57.	            //如果这个位置能放置皇后

58.	            if (isValidation(result, row, j)) {

59.	                //记录放置坐标

60.	                result[row] = j;

61.	                //放置下一行

62.	                backtracking(result, row + 1);

63.	            }

64.	        }

65.

66.	    }

67.

68.	    // 验证，无同行/同列棋子

69.	    // 对角线无棋子

70.	    private boolean isValidation(int[] result, int row, int col) {

71.	        for (int i = 0; i < row; i++) { // 第一行可以放任意位置

72.	            int sub = row - i; // 行数差

73.	            // 如果同列、同对角线出现皇后，说明不能在row col放置皇后

74.	            if (result[i] == col || result[i] == col - sub || result[i] == col + sub) {

75.	                return false;

76.	            }

77.	        }

78.	        //检测结束后能放置

79.	        return true;

80.	    }

输出结果

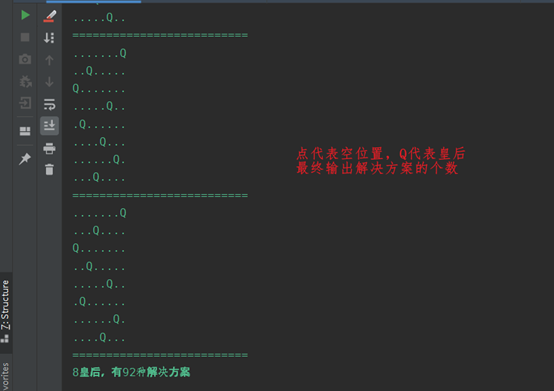
算法分析

N 皇后问题的解空间是一棵n叉树，树的深度是n，最坏情况下解空间树深度是n，除了根节点和叶子结点，其余结点的子节点有n个分支，总分枝的个数是n^{n，每个分支都判断约束函数，判断约束条件需要O(n)的时间，因此耗时需要O(n}(n+1))，所以时间复杂度是O(n^(n+1));

回溯法的另一个重要特性是在搜索执行的同时产生解空间，从开始结点起最长的路径是n，我们声明的result数组大小是n，用来保存皇后的坐标。所以该算法的空间复杂度是O(n)。

回溯法算是一种选优搜索法，按照选优条件深度优先搜索，达到目标，当搜索到某一步时，发现原先选择不是目标或者不是最优就退回重新选择。这种方法通过剪枝来减少递归的次数。如果超时的话可以换其他方法解决。