概念定义：

P问题：能在多项式时间内解决的问题；

NP问题：（Nondeterministic Polynomial time Problem）不能在多项式时间内解决或不确定能不能在多项式时间内解决，但能在多项式时间内验证的问题；

NPC问题：（NP Complete）NP完全问题，所有NP问题在多项式时间内都能规约（Reducibility）到它的NP问题，即解决了此NPC问题，所有NP问题也都能得到解决；

NP hard问题：NP难问题，所有NP问题在多项式时间内都能规约（Reducibility）到它的问题，但不一定是NP问题。

概念图解：

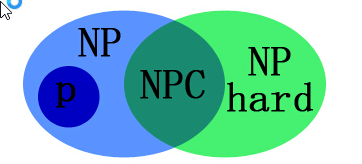
说明：

  1. P问题属于NP问题，NPC问题属于NP问题；
  2. NPC问题同时属于NP hard问题，是NP与NP hard问题的集合。

概念应用：

NPC问题有很多的，比较有名的有团问题，顶点覆盖集问题，支配集问题，独立集问题，哈密顿路问题，旅行商问题等，同样有很多是NP-hard而不是NPC的问题，比如围棋，停机问题等。

更多信息，请参考阅读：

http://www.matrix67.com/blog/archives/105

http://www.cnblogs.com/jpcflyer/archive/2012/04/15/2450622.html

（数学）P、NP、NPC、NP hard问题的更多相关文章

  1. P,NP,NPC的通俗解释

    这或许是众多OIer最大的误区之一.    你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这个只有搜了,这已经被证明是NP问题 了”之类的话.你要知道,大多数人此时所说的NP问题其实都是指的N ...

  2. 算法复习-P NP NPC NP-hard概念

    from http://blog.csdn.net/huang1024rui/article/details/49154507 P.NP.NPC和NP-Hard相关概念的图形和解释 一.相关概念 P: ...

  3. P,NP,NPC,NPC-HARD

    P: 能在多项式时间内解决的问题 NP: 不能在多项式时间内解决或不确定能不能在多项式时间内解决,但能在多项式时间验证的问题 NPC: NP完全问题,所有NP问题在多项式时间内都能约化(Reducib ...

  4. 区分range() , np.arange() , np.linspace()

    content: range() np.arange() np.linspace() 一.range(start, stop, step) 1.range() 为 python 自带函数 2.生成一个 ...

  5. scikit-learn工具学习 - random,mgrid,np.r_ ,np.c_, scatter, axis, pcolormesh, contour, decision_function

    yuanwen: http://blog.csdn.net/crossky_jing/article/details/49466127 scikit-learn 练习题 题目:Try classify ...

  6. Python 中的几种矩阵乘法 np.dot, np.multiply, *【转】

    本文转载自:https://blog.csdn.net/u012609509/article/details/70230204 Python中的几种矩阵乘法1. 同线性代数中矩阵乘法的定义: np.d ...

  7. Numpy：np.vstack()&np.hstack() flat/flatten

    一 .  np.vstack: 按垂直方向(行顺序)堆叠数组构成一个新的数组 In[3]: import numpy as np In[4]: a = np.array([[1,2,3]]) a.sh ...

  8. Python 中的几种矩阵乘法 np.dot, np.multiply, *

    使用array时,运算符 * 用于计算数量积(点乘),函数 dot() 用于计算矢量积(叉乘).使用matrix时,运算符 * 用于计算矢量积,函数 multiply() 用于计算数量积. 下面是使用 ...

  9. numpy-np.ceil,np.floor,np.expand_dims方法

    np.ceil(多维数组):对多维数组的各个数向上取整 np.floor(多维数组):对多维数组的各个数向下取整 np.expand_dims(x,axis = 0):在x的第一维度上插入一个维度,a ...

随机推荐

  1. OS 系统下安装MySql 配置MySql环境变量

    学习Hive需要,闲话不说 本文的内容: 下载Mysql for Mac 下载Mysql Workbench 安装 Mysql 和 Mysql Workbench 配置Mysql在OS 系统上的环境变 ...

  2. python核心编程笔记

    1.python的对象是通过引用传递的. 2.多元赋值: x, y = y, x

  3. 动态加载js文件

    由于最近在弄echarts,关于地图类的效果,但是全国地图整体的js文件太大了,加载很耗费资源,所以要根据不同省份加载不同地区的js地图, 于是就想的比较简单, var script = docume ...

  4. 如何定制Activity的标题栏

    requestWindowFeature(Window.FEATURE_CUSTOM_TITLE); setContentView(R.layout.main); //自定义标题栏        mW ...

  5. Mini projects #4 ---- Pong

    课程全名:An Introduction to Interactive Programming in Python,来自 Rice University 授课教授:Joe Warren, Scott ...

  6. 在c#中使用bitblt显示图片

    使用bitblt比DrawImage有更好的性能 using AForge.Video.DirectShow; using System; using System.Collections.Gener ...

  7. 【转】【WebDriver】不可编辑域和日历控件域的输入 javascript

    http://blog.csdn.net/fudax/article/details/8089404 今天用到日历控件,用第一个javascript执行后页面上的日期控件后,在html中可以看到生效日 ...

  8. wangEditor ie9 表单上传图片

    wangEditor ie9 表单上传图片  弹框无法消失  var resultText = $.trim(iframeWindow.document.body.innerHTML); result ...

  9. Spring 使用JSTL标签显示后台数据

    1. 先上项目结构图,其中config包下的代码文件参见前一篇博客   http://www.cnblogs.com/njust-ycc/p/6123505.html 引包: 2. 主要代码 (1)U ...

  10. 用脚本定时监控SQL Server主从一致性

    用脚本定时监控SQL Server主从一致性 首先说一下我们的环境 我们使用的是事务复制,复制是单向的,主服务器和从服务器都在同一个机房,当然不同机房也可以,只需要改一下IP和端口 下面的脚本在我们的 ...