TRI 解题报告

题目大意：

在一个平面上有N(N <= 1000)个点，其中任意三点不共线，求这些点组成的三角形的面积和每和三角形内部含的点数的个数和。

数据范围：

20%的数据 N <= 50, 30% N <= 100, 100% N <= 1000。

算法讨论

算法1：

看到这题还是有部分分的，那么我们首先映入脑袋中的就是O(N^4)的算法，暴力枚举三个点叉积算面积，然后再枚举剩下的点判断是否在当前的三角形内。

如何判断一个点在三角形内部，有个不错的教程：http://www.yalewoo.com/in_triangle_test.html

考场上打这个暴力还是30分妥妥的。

算法2：

O(N^2logn)。

首先对于第一问：

我们考虑，对于一条边来说，边外的点都能和其组成一个三角形，而在枚举边的过程中，可能会对一个三角形多次计算，所以为了避免这种重复计算，我们就要保证一定的顺序，做到不重不漏。于是，对于这样的散点图，我们经常用到的排序方法有两种，第一个是以x为第一关键字，以y为第二关键字进行排序，另一个就是极角排序。（至于不知道什么是极角的，自行百度）。

我们枚举每一个点让其做为一个边的起点，然后以这个点为基准进行极角排序（两种方法，一个是让其它点的坐标都减去这个点的坐标，然后atan2，另一个就是用这个点与其它点的斜率），下面给出这样一个过程。

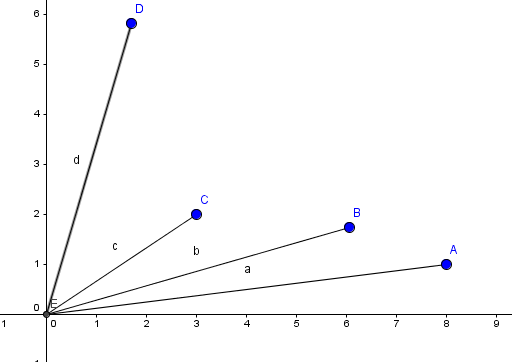我们看这样一张图，如果计算S（AOB） + S(AOC) + S(AOD)，那么这个面积和就等于 OA叉OB +　OA叉OC　＋　OA叉OD

就等于　　－　ｘｂ　＊　ｙａ　＋　ｘａ　＊　ｙｂ　－　ｘｃ　＊　ｙａ　＋　ｘａ　＊　ｙｃ　－　ｘｄ　＊　ｙａ　＋　ｘａ　＊　ｙｄ　＝　－（ｘｂ　＋　ｘｃ　＋　ｘｄ）　＊　ｙａ　＋　ｘａ　＊　（ｙｃ　＋　ｙｄ　＋　ｙｂ），为了保证这个结合是成立的，我们必须保证上面计算的顺序，也要保证都是向左旋，这样叉积才是正的。所以我们对于每一个点为基准，然后枚举那个‘Ａ＇，就可以得到以每个点为端点的每一个三角形的面积。然后想办法减少计算的重复，就需要极角排序一下。

对于第二问，我们考虑，当我们每选定一个点的时候，那么它最多在Ｃ（２，ｎ－１）个三角形中，我们采用补集的思想，当且仅当三个点在这个点同侧的时候，这个点不在三个点围成的三角形中，那么，假设我们当前找的基准点是A，那么已经枚举的那个点是Ａ＇，我们只要统计ＡＡ＇一侧的点的数量就可以了，然后组合计数　Ｃ（２，．．．），计算得出答案。同样，为了避免重复，　我们要按照一定的顺序就ＯＫ了。

Codes：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <cstdlib>
 #include <algorithm>
 #include <cmath>
 using namespace std;
 typedef long long ll;

 int n;
 struct Point{
     double x, y, ji;

     Point(double _x = , double _y = ): x(_x), y(_y) {}
     bool operator < (const Point &a) const{
         return ji < a.ji;
     }
 }p[ * ], T[];

 int C(int x, int y){
     int ret = ;
     for(int i = y; i > y-x; -- i){
         ret = ret * i;
     }
     for(int i = ; i <= x; ++ i)
         ret = ret / i;
     return ret;
 }

 double Cross(Point a, Point b){
     return a.x * b.y - a.y * b.x;
 }

 void Solve(){
     ll ans1 = , ans2 = ;
     for(int i = ; i <= n; ++ i){
         int cnt = ;
         for(int j = ; j <= n; ++ j){
             if(j != i){
                 ++ cnt;
                 p[cnt].x = T[j].x - T[i].x; p[cnt].y = T[j].y - T[i].y;
                 p[cnt].ji = atan2(p[cnt].y, p[cnt].x);
             }
         }
         sort(p + , p + cnt + );
         for(int j = ; j <= cnt; ++ j)
             p[cnt + j] = p[j];
         ans2 += C(, cnt);
         for(int j = , k = ; j <= cnt; ++ j){
             if(j == k) k ++;
             while(Cross(p[j], p[k]) > ) k ++;
             Point tp(T[i].x + p[j].x, T[i].y + p[j].y);
             ans1 += (long long)Cross(T[i], tp) * (k - j - );
             ans2 -= (long long)(k - j - ) * (k - j - ) / ;
         }
     }
     printf("%lf %lf\n", (double) ans1 /  / C(, n), (double) ans2 / C(, n));
 }
 #define ONLINE_JUDGE
 int main(){
 #ifndef ONLINE_JUDGE
     freopen("tri.in", "r", stdin);
     freopen("tri.out", "w", stdout);
 #endif

     scanf("%d", &n);
     for(int i = ; i <= n; ++ i){
         scanf("%lf%lf", &T[i].x, &T[i].y);
     }

     Solve();

 #ifndef ONLINE_JUDGE
     fclose(stdin); fclose(stdout);
 #endif
     return ;
 }

TRI