count(*)实现原理+两阶段提交总结

count(*)实现原理

• 不同引擎的实现：
  • MyISAM引擎把表的总行数存在了磁盘上，执行COUNT(*)就会直接返回，效率很高；
  • InnoDB在count(*)时，需要把数据一行一行的从引擎里面取出来然后累计记数。
  • 注意如果有where过滤条件MYISAM速度就不是很快了。

• 为什么Innodb不和MYISAM一样？

  • 根本原因：即使在同一时刻的多个查询，由于MVCC的原因，Innodb对于应该返回多少行也是不确定的，比如以下场景例子（设计了三个用户并行会话）：

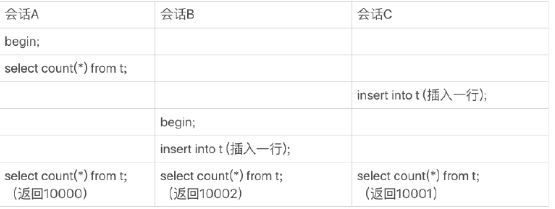
    • 会话A先启动事物并查询一次表的总行数；
    • 会话B启动事物，插入一行记录后，查询表的总行数
    • 会话C启动一个单独语句，插入一行记录后，查询表的总行数。

  • 假设从上到下是按时间顺序执行的，同一行语句，在同一时刻执行，拿到的数据却是不一样的。

    • 

    • 解决方法：

      • 

      • 虽然会话B的读操作仍然是在T3执行的，但是因为这时候更新事务还没有提交，所以计数值加1这个操作对会话B还不可见。

• count(*),count(主键),count(1),count(字段)区别

  • count(id) ：Innodb会遍历整张表，把每一行的id都取出来，返回给server，server层拿到id后，判断是不可能为空的，按行累加。
  • count(1)：innodb遍历整张表，但不取值，server层对于返回的每一行，放一个数字1进去，判断是不肯能为空的，按行累加。
  • count(字段)：
    • 如果这个字段定义为not null的话，一行行从记录里读出这个字段，判断不能为null，按行累加
    • 如果允许为null的话，执行的时候，判断到有可能是null，还要把值取出来判断以下，不是null才累加。
  • count()：并不会把全部字段取出来，而是专门做了优化，不取值。count(*)肯定不
    是null，按行累加。

  所以结论是：按照效率排序的话，count(字段)<count(主键id)<count(1)≈count(‘*’)，所以我建议你，尽量使用count(*)。

两阶段提交MYSQL异常重启会出现什么现象

• 

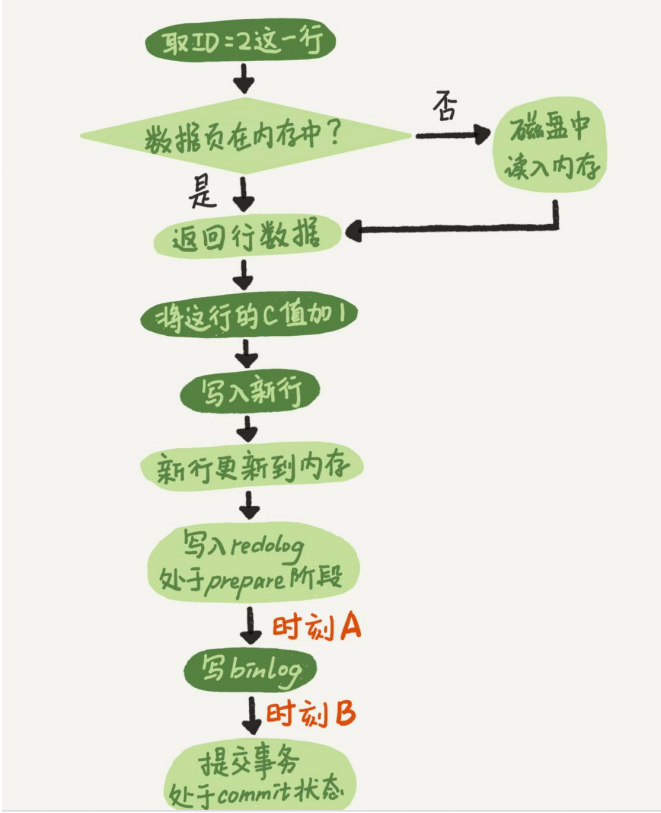
• 如果在图中时刻A的地方，也就是写入redo log 处于prepare阶段之后、写binlog之前，发生了崩

  溃（crash），由于此时binlog还没写，redo log也还没提交，所以崩溃恢复的时候，这个事务会

  回滚。这时候，binlog还没写，所以也不会传到备库。

• 主要集中在时刻B，也就是binlog写完，redo log还没commit前发生 crash，那崩溃恢复的时候MySQL会怎么处理？

  • 崩溃恢复时的判断规则
    1. 如果redo log里面十五是完整的，也就是已经有了commit表示，则直接提交
    2. 如果redo log里面的十五只有完整的prepare，则判断对应事物的binlog是否完整，是则提交，否则回滚
  • 所以在B时刻崩溃食物会被提交。

• MySQL是怎么知道binlog完整的？

  • 一个事务的binlog是有完整格式的：statement格式的binlog，最后会有COMMIT；row格式的binlog，最后会有一个XID event。
• redo log和binlog是怎么关联起来的
  • 它们有一个共同的数据字段，叫XID。崩溃恢复的时候，会按顺序扫描redo log：
  • 如果碰到既有prepare、又有commit的redo log，就直接提交；
  • 如果碰到只有parepare、而没有commit的redo log，就拿着XID去binlog找对应的事务。

• 为甚么要两阶段提交

  • 对于InnoDB引擎来说，如果redo log提交完成了，事务就不能回滚（如果这还允许回滚，就可能 覆盖掉别的事务的更新）。而如果redo log直接提交，然后binlog写入的时候失败，InnoDB又回 滚不了，数据和binlog日志又不一致了。

    两阶段提交就是为了给所有人一个机会，当每个人都说“我ok”的时候，再一起提交。

• 正常运行中的实例，数据写入后的最终落盘，是从redo log更新过来的还是从 buffffer pool更新过来的呢？
  • redo log并没有记录数据页的完整数据，所以它并没有能力自己去更新磁盘数据页，也就不存在“数据最终落盘，是由redo log更新过去”的情况。
    1. 如果是正常运行的实例的话，数据页被修改以后，跟磁盘的数据页不一致，称为脏页。最终 数据落盘，就是把内存中的数据页写盘。这个过程，甚至与redo log毫无关系。
    2. 在崩溃恢复场景中，InnoDB如果判断到一个数据页可能在崩溃恢复的时候丢失了更新，就会将它读到内存，然后让redo log更新内存内容。更新完成后，内存页变成脏页，就回到了第 一种情况的状态。