由于sha1签名算法进入淘汰阶段，逐渐弃用中，sha1升级为sha2是大势所趋。

微软已经正式发布sha1弃用策略： http://blogs.technet.com/b/pki/archive/2013/11/12/sha1-deprecation-policy.aspx

谷歌没多久也发布sha1的日落计划： http://blog.chromium.org/2014/09/gradually-sunsetting-sha-1.html

下面我们来关注几个重要的日子：

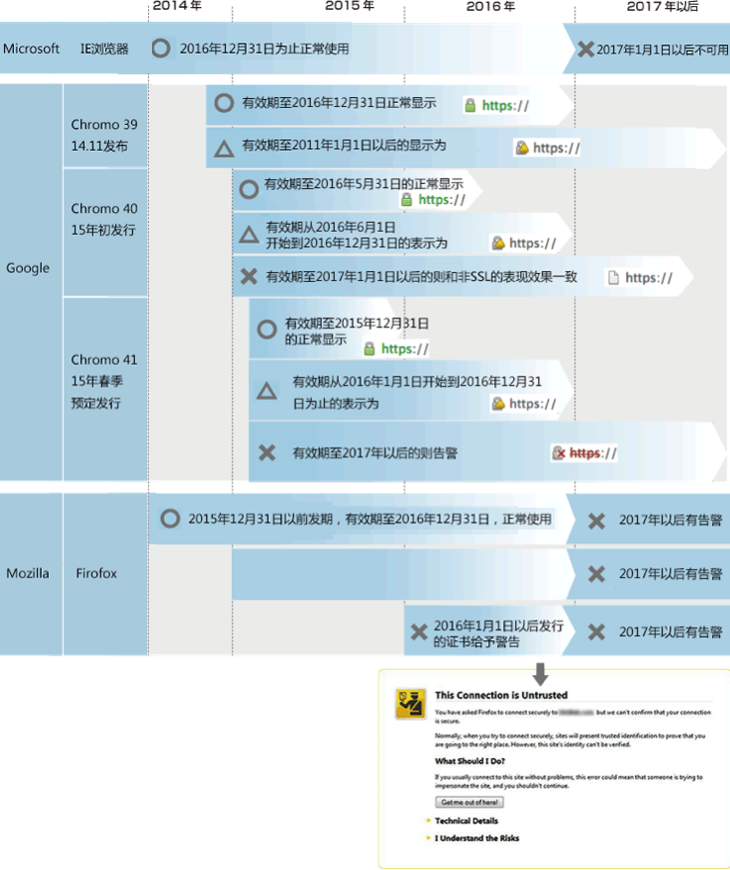
2014年9月，2017后依然未过期的sha1证书，chrome将给予告警

2014年12月，2016年6月1日以后过期的sha1证书，chrome给予告警

2015年2月，任意2016年以后仍生效的sha1证书，chrome给予告警。

2016年1月，微软将不信任不带时间戳的sha1的代码签名。

2017年1月，微软和Mozilla都将不再信任sha1的ssl证书。

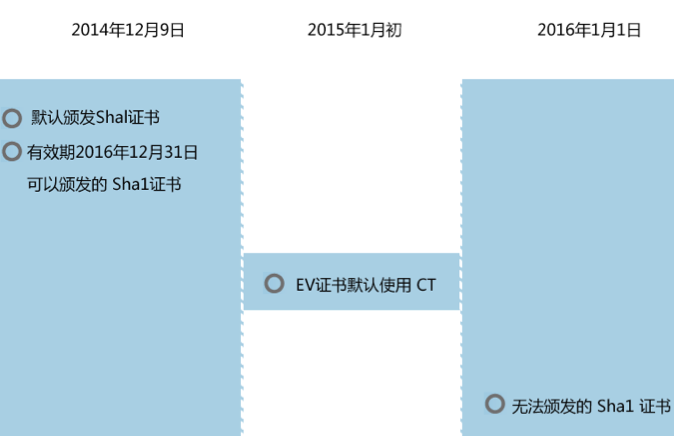
针对sha2的升级策略，我们易维信做出如下方案：

在2014年12月份，默认签发sha2的证书，在此期间，如果不是2017年前仍生效的证书，可选择重颁发sha1证书。2016年1月1日以后，不再发出任何sha1证书

sha2 替换sha1 时间表的更多相关文章

  1. Microsoft 根证书计划弃用 SHA-1 哈希算法

    Microsoft 根证书计划弃用 SHA-1 哈希算法 微软官方2016年1月12日发布安全通报,自2016年1月1日起Microsoft 已经发布代码弃用变更,也就是说2016年1月1号后用SHA ...

  2. 密码学系列之:NIST和SHA算法

    目录 简介 SHA1 SHA2 SHA3 简介 SHA算法大家应该都很熟悉了,它是一个用来计算hash的算法,目前的SHA算法有SHA1,SHA2和SHA3种.这三种算法都是由美国NIST制定的. N ...

  3. git版本管理策略及相关技巧(A)

    公司几乎所有的项目都是使用 git 仓库来管理代码,以前对 git 只有些肤浅的了解,每次提交代码或者上线的时候总是会提心吊胆,生怕出现一些未知的问题.经过三个月的踩坑和填坑, git 操作颇显成熟. ...

  4. Git for Windows v2.11.0 Release Notes

    homepage faq contribute bugs questions Git for Windows v2.11.0 Release Notes Latest update: December ...

  5. 转 git操作小结

    UNDER MIT LICENSE. 公司几乎所有的项目都是使用 git 仓库来管理代码,以前对 git 只有些肤浅的了解,每次提交代码或者上线的时候总是会提心吊胆,生怕出现一些未知的问题.经过三个月 ...

  6. MD5碰撞后时代，MD5还有存在的意义吗？

    MD5是一种HASH函数,又称杂凑函数,由32位16进制组成,在信息安全范畴有广泛和首要运用的暗码算法,它有类似于指纹的运用.在网络安全协议中, 杂凑函数用来处理电子签名,将冗长的签名文件紧缩为一段一 ...

  7. SHA安全散列算法简析

    1 SHA算法简介 1.1 概述 SHA (Secure Hash Algorithm,译作安全散列算法) 是美国国家安全局 (NSA) 设计,美国国家标准与技术研究院(NIST) 发布的一系列密码散 ...

  8. SSL加速卡调研的原因及背景

    SSL加速卡调研的原因及背景 SSL加速卡调研的原因及背景 网络信息安全已经成为电子商务和网络信息业发展的一个瓶颈,安全套接层(SSL)协议能较好地解决安全处理问题,而SSL加速器有效地提高了网络安全 ...

  9. md5sum 和 sha256sum用于 验证软件完整性

    md5sum 和 sha256sum 都用来用来校验软件安装包的完整性,本次我们将讲解如何使用两个命令进行软件安装包的校验: sha 是什么?        sha 为 安全散列算法(英语:Secur ...

随机推荐

  1. Codeforces--400A--Inna and Choose Options（模拟水题）

    Inna and Choose Options Crawling in process... Crawling failed Time Limit:1000MS     Memory Limit:26 ...

  2. 54. Extjs组件render说明

    转自:http://blog.chinaunix.net/uid-450400-id-2119168.html 1. 1.调用组件的render方法 panel.render('div'); 2.在配 ...

  3. Knights of the Round Table(Tarjan+奇圈)

    http://poj.org/problem?id=2942 题意:n个武士,某些武士之间相互仇视,如果在一起容易发生争斗事件.所以他们只有满足一定的条件才能参加圆桌会议:(1)相互仇视的两个武士不能 ...

  4. 慕课网6-2 作业：js实现轮播特效

    小伙伴们,掌握了JavaScript的语法.流程控制语句.内置对象以及DOM和BOM的知识,运用所学知识完成如下图所示的交互效果——轮播图.效果图如下: 具体交互效果图参考gif动态效果图,gif效果 ...

  5. Java高质量20问

    问题一:在多线程环境中使用HashMap会有什么问题?在什么情况下使用get()方法会产生无限循环? HashMap本身没有什么问题,有没有问题取决于你是如何使用它的.比如,你在一个线程里初始化了一个 ...

  6. $luogu2375[NOI2014]$

    \(problem\) 其中,\(next[i],next[next[i]],next[next[next[i]]]......\)都是这个前缀串i的公共前后缀,而且只有它们是公共前后缀 那么,我们其 ...

  7. 【洛谷3224/BZOJ2733】[HNOI2012]永无乡 (Splay启发式合并)

    题目: 洛谷3224 分析: 这题一看\(n\leq100000\)的范围就知道可以暴力地用\(O(nlogn)\)数据结构乱搞啊-- 每个联通块建一棵Splay树,查询就是Splay查询第k大的模板 ...

  8. 了解MySQL的字符集

    在数据库中,字符乱码属于常见.多发问题.鉴于本人水平顶多只能归于不入流之类,写这篇文章时内心诚惶诚恐,实在担心误导大家.内容仅供参考,若有错误,请各位及时指出,我也好学习提高! MySQL的字符集有4 ...

  9. 表格对象的获取和更改（原生js）

    表格对象的获取 var oT = document.getElementById("tb"); //获取head console.log(oT.tHead); console.lo ...

  10. Android 微信SDK图片分享（checkArgs fail, thumbData is invalid）

    微信官网给的Demo中.图片的分享例子他是这么描述的: String url = "http://pic2.nipic.com/20090506/1478953_125254084_2.jp ...