《统计学习方法》笔记九 EM算法及其推广
本系列笔记内容参考来源为李航《统计学习方法》
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计或极大后验概率估计。迭代由
(1)E步:求期望
(2)M步:求极大
组成,称为期望极大算法。
EM算法引入




EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。

EM在监督学习中的应用

收敛性


EM算法在高斯混合模型学习中的应用
高斯混合模型

高斯混合模型参数估计的EM算法


EM算法的推广
EM算法还可解释为F函数的极大-极大算法,基于这个解释有若干变形与推广。
首先引入F函数的概念

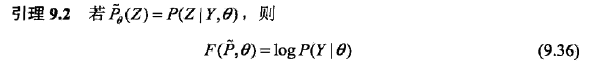





《统计学习方法》笔记九 EM算法及其推广的更多相关文章
- EM算法及其推广
概述 EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计. EM算法的每次迭代由两步组成:E步,求期望(expectation): ...
- 统计学习方法笔记--EM算法--三硬币例子补充
本文,意在说明<统计学习方法>第九章EM算法的三硬币例子,公式(9.5-9.6如何而来) 下面是(公式9.5-9.8)的说明, 本人水平有限,怀着分享学习的态度发表此文,欢迎大家批评,交流 ...
- python机器学习笔记:EM算法
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域的基础,比如隐式马尔科夫算法(HMM),LDA主题模型的变分推断算法等等.本文对于E ...
- GMM高斯混合模型学习笔记(EM算法求解)
提出混合模型主要是为了能更好地近似一些较复杂的样本分布,通过不断添加component个数,能够随意地逼近不论什么连续的概率分布.所以我们觉得不论什么样本分布都能够用混合模型来建模.由于高斯函数具有一 ...
- 统计学习方法笔记 -- KNN
K近邻法(K-nearest neighbor,k-NN),这里只讨论基于knn的分类问题,1968年由Cover和Hart提出,属于判别模型 K近邻法不具有显式的学习过程,算法比较简单,每次分类都是 ...
- EM算法及其推广的要点
1.EM算法是含有隐变量的变量的概率模型极大似然估计或极大后验概率估计的迭代算法,含有隐变量的概率模型的数据表示为$P(Y,Z|\theta)$.这里,$Y$是观测变量的数据,$Z$是隐变量的数据,$ ...
- 【机器学习笔记】EM算法及其应用
极大似然估计 考虑一个高斯分布\(p(\mathbf{x}\mid{\theta})\),其中\(\theta=(\mu,\Sigma)\).样本集\(X=\{x_1,...,x_N\}\)中每个样本 ...
- 统计学习方法笔记(KNN)
k近邻法(k-nearest neighbor,k-NN) 输入:实例的特征向量,对应于特征空间的点:输出:实例的类别,可以取多类. 分类时,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预 ...
- 统计学习方法笔记 -- Boosting方法
AdaBoost算法 基本思想是,对于一个复杂的问题,单独用一个分类算法判断比较困难,那么我们就用一组分类器来进行综合判断,得到结果,"三个臭皮匠顶一个诸葛亮" 专业的说法, 强可 ...
随机推荐
- iOS开发过程中 xcode文件与Finder中文件保持一致 + 支付宝集成出错
目录 环境 前言 1.使用 Gem 安装 synx 2.直接在终端 Terminal 中开始使用 3.在使用的时候还可以加参数来实现不同的功能 4.解决项目中出现的一些 error 环境 OS X 1 ...
- Codeforces Round #373 (Div. 2) C. Efim and Strange Grade —— 贪心 + 字符串处理
题目链接:http://codeforces.com/problemset/problem/719/C C. Efim and Strange Grade time limit per test 1 ...
- 追求代码质量: 用 AOP 进行防御性编程
原文出处: IBM中国 开发人员测试的主要缺点是:绝大部分测试都是在理想的场景中进行的.在这些情况下并不会出现缺陷 —— 能导致出现问题的往往是那些边界情况. 什么是边界情况呢?比方说,把 null ...
- 对xml文件的sax解析(增删改查)之一
crud(增删改查): c:creat r:retrieve u:update d:delete 以下笔记来自于韩顺平老师的讲解. 现在是用java来操作. 第一步:新建java工程.file-new ...
- Log4j输出格式控制--log4j的PatternLayout参数含义
参数 说明 例子 %c 列出logger名字空间的全称,如果加上{<层数>}表示列出从最内层算起的指定层数的名字空间 log4j配置文件参数举例 输出显示媒介 假设当前logger名字 ...
- 【错误信息】springMVC No mapping found for HTTP request with URI
出现这个问题的原因是在web.xml中配置错了:
- PHP中的关系判断和注释
== 只判断内容,不判断类型=== 全等于,即判断内容,又判断类型 != 不等于,只判断内容,不判断类型 !== 全不等于,即判断内容,又判断类型
- MySQL丨分页查询
直奔主题 一.sql语句:select * from table limit startPageNum,everyPageNum 1)语句解析: table:你要查询的表 startPageNum:从 ...
- 【C】由printf("%d\t%d\t%d\n",a,a+=(a++),a);引起的思考
#include<stdio.h> int main() { ,a1=; ,b1=; printf("(1)后自加:\n"); printf("a+=(a++ ...
- python库学习笔记——分组计算利器:pandas中的groupby技术
最近处理数据需要分组计算,又用到了groupby函数,温故而知新. 分组运算的第一阶段,pandas 对象(无论是 Series.DataFrame 还是其他的)中的数据会根据你所提供的一个或多个键被 ...
