【绝迹篇】C#RSA算法实现

当下最流行的RSA加密算法,只有公钥和私钥同时拥有才能破解加密信息,RSA加密算法的出现有利于数据安全性传输

1.C#中自带RSACryptoServiceProvider类可以让你很好的生成XML格式的公钥和私钥,两句代码就搞定

2.但是生成的XML格式前端不能很好的利用和读懂,所以在生成的XML格式里需要转换成PEM格式,这样才能直接Copy到验证工具里加密解密,非常方便

首先,我们先导入一个第三方库,因为下面涉及到的转换代码都是需要依赖这个库来实现,导入操作如下

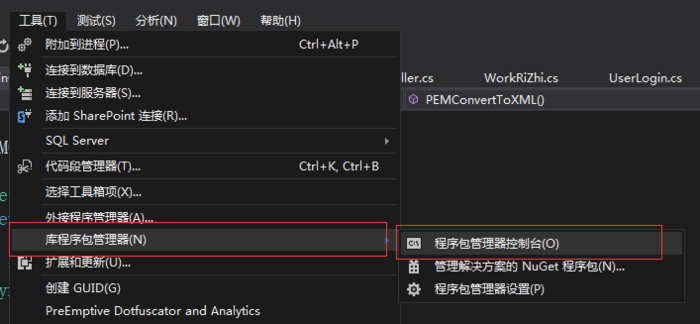
控制台里输入

PM > Install-Package BouncyCastle

导入到引用里面

3.好了,下面就是纯代码实现了,目的就是将XML格式转换为PEM格式,无论公钥还是私钥,不罗嗦直接代码走起

        static void Main(string[] args)
        {
            RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();
            string xmlPrivateKey = rsa.ToXmlString(true);//XML密钥
            string pemPrivateKey = Xml2PemPrivate(xmlPrivateKey, "F:/privatePEM.txt");//PEM密钥

            string xmlPublicKey = rsa.ToXmlString(false);//XML公钥
            string pemPublicKey = Xml2PemPublic(xmlPublicKey, "F:/publicPEM.txt");//PEM公钥
        }

        /// <summary>
        ///  XML格式公钥转PEM格式公钥
        /// </summary>
        /// <param name="xml">XML格式的公钥</param>
        /// <param name="saveFile">保存文件的物理路径</param>
        public static string Xml2PemPublic(string xml, string saveFile)
        {
            var rsa = new RSACryptoServiceProvider();
            rsa.FromXmlString(xml);
            var p = rsa.ExportParameters(false);
            RsaKeyParameters key = new RsaKeyParameters(false, new BigInteger(1, p.Modulus), new BigInteger(1, p.Exponent));
            using (var sw = new StreamWriter(saveFile))
            {
                var pemWriter = new Org.BouncyCastle.OpenSsl.PemWriter(sw);
                pemWriter.WriteObject(key);
            }

            SubjectPublicKeyInfo publicKeyInfo = SubjectPublicKeyInfoFactory.CreateSubjectPublicKeyInfo(key);
            byte[] serializedPublicBytes = publicKeyInfo.ToAsn1Object().GetDerEncoded();
            string publicKey = Convert.ToBase64String(serializedPublicBytes);
            return Format(publicKey, 1);
        }

        /// <summary>
        ///  XML格式私钥转PEM
        /// </summary>
        /// <param name="xml">XML格式私钥</param>
        /// <param name="saveFile">保存文件的物理路径</param>
        public static string Xml2PemPrivate(string xml, string saveFile)
        {
            var rsa = new RSACryptoServiceProvider();
            rsa.FromXmlString(xml);
            var p = rsa.ExportParameters(true);
            var key = new RsaPrivateCrtKeyParameters(
                new BigInteger(1, p.Modulus), new BigInteger(1, p.Exponent), new BigInteger(1, p.D),
                new BigInteger(1, p.P), new BigInteger(1, p.Q), new BigInteger(1, p.DP), new BigInteger(1, p.DQ),
                new BigInteger(1, p.InverseQ));
            using (var sw = new StreamWriter(saveFile))
            {
                var pemWriter = new Org.BouncyCastle.OpenSsl.PemWriter(sw);
                pemWriter.WriteObject(key);
            }

            PrivateKeyInfo privateKeyInfo = PrivateKeyInfoFactory.CreatePrivateKeyInfo(key);
            byte[] serializedPrivateBytes = privateKeyInfo.ToAsn1Object().GetEncoded();
            string privateKey = Convert.ToBase64String(serializedPrivateBytes);
            return Format(privateKey, 2);
        }

        /// <summary>
        ///  格式化公钥/私钥
        /// </summary>
        /// <param name="key">生成的公钥/私钥</param>
        /// <param name="type">1:公钥 2:私钥</param>
        /// <returns>PEM格式的公钥/私钥</returns>
        public static string Format(string key, int type)
        {
            string result = string.Empty;

            int length = key.Length / 64;
            for (int i = 0; i < length; i++)
            {
                int start = i * 64;
                result = result + key.Substring(start, 64) + "\r\n";
            }

            result = result + key.Substring(length * 64);
            if (type == 1)
            {
                result = result.Insert(0, "-----BEGIN PUBLIC KEY-----\r\n");
                result += "\r\n-----END PUBLIC KEY-----";
            }
            if (type == 2)
            {
                result = result.Insert(0, "-----BEGIN PRIVATE KEY-----\r\n");
                result += "\r\n-----END PRIVATE KEY-----";
            }

            return result;
        }

4.最后输出在F盘的TXT文件里面就是可以直接用来Copy到验证工具里面直接加密/解密数据用的