【读书笔记】周志华《机器学习》第三版课后习题讨<第一章-绪论>

虽然是绪论。。但是。。。真的有点难！不管怎么说，一点点前进吧。。。

声明一下答案不一定正确，仅供参考，为本人的作答，希望大神们能多多指教~

1.1 表1.1中若只包含编号为1和4的两个样例，试给出相应的版本空间。

解答：本题考查版本空间、假设空间的概念。简而言之，假设空间是该问题情景下，所有的取值可能性（包括单属性泛化、二属性泛化、X属性泛化……全泛化的情况），而版本空间则是指在测试用样本情境下，满足样本内所有正例的假设集合（一般版本空间内的假设都是带有属性泛化）。

我们先来看一下1和4样例组成的表，以供接下来探讨进行参考：

编号	色泽	根蒂	敲声	好瓜？
1	青绿	蜷缩	浊响	是
4	乌黑	稍蜷	沉闷	否

解题中，要紧扣“我只知道这张表的信息，去推测整体”的思想。根据此表信息，假设空间是（2+1）X（2+1）X（2+1）+1=28种假设，版本空间则应该是假设空间内能确定1是好瓜，同时刚好能排除4是好瓜的所有可能，所以应该是（色泽=青绿）∧（根蒂=蜷缩）∧（敲声=浊响），以及本例的一个属性泛化（三种），和两个属性泛化（三种），共7种。不可加入三属性泛化，因为（色泽=*）∧（根蒂=*）∧（敲声=*），这种情况会把编号4也判定为好瓜，与样本不符。

1.2 与使用单个合取式来进行假设表示相比，使用“析合范式”将使得假设空间具有更强的表示能力。若使用最多包含K个合取式的析合范式来表达表1.1西瓜分类问题的假设空间，试估算共有多少种可能的假设。

解答：本题考查一些离散数学的知识，同时为后文提示了使假设空间具有更强表示能力的一种编程表达。我们再来看一下表1.1：

编号	1	2	3	4
色泽	青绿	乌黑	青绿	乌黑
根蒂	蜷缩	蜷缩	硬挺	稍蜷
敲声	浊响	浊响	清脆	沉闷
好瓜	是	是	否	否

根据此表，总共有三种属性，每种属性分别有2，3，3种取值。根据假设空间计算式，应该有3X4X4+1=49种可能假设。由于问了几个人都不确定空集是否加入析合范式，所以下文讨论除去空集，48种假设。

其中，题设要求的析合范式，无非就是若干个上述假设的组合。可以理解为上述48种假设挑一种，挑2种，挑3种……挑48种，以此类推。不考虑冗余情况，很容易推算出以下的公式：

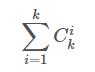
该公式计算出的值减1即可（不减1则是把空集包含在析合范式内的情况），同时，这个式子的值也等于2的K次方。

但是，要考虑冗余情况。根据离散数学的知识，如果（A=a)∨(A=*),则该项可以化简成(A=*).那么上式包括的结果内，会包含大量冗余。经过计算，这个问题在总假设可能在48种的情况下，远没有2的48次方这么大的量。具体的计算将会在另外一片文章内说明：

C++实现：对于48种假设情况的计算

1.3 若数据包含噪声，则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下，试设计一种归纳偏好用于假设选择。

解答：题目换一种意思就是，可能无法找到一种标准，既能区分所有正例，也能排除所有反例。相当于还是一个过拟合和欠拟合的一个问题引入。这个问题是一定没有标准答案的。思路两种，一种，设定一个阈值，对大部分属性与训练样本正例一致的反例，也划入正例范畴。另外一种就是，只取最核心、最无异议的正例进行区分。这里不详述。

1.4 本章1.4节在讨论NFL（没有免费的午餐的英文缩写）定理时，默认使用了分类错误率作为性能度量来对分类器进行评估，若换用其他性能度量l，则式1.1将改为：

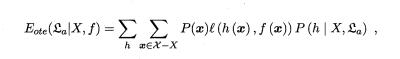试依然证明“天下没有免费的午餐”。

解答：不会不会。。。放弃。。。好好去看概率论去。。。

1.5 试简述机器学习能在互联网搜索的哪些环节起到什么作用？

解答：开放题，不多bb