python全栈开发笔记---------数据类型-----集合set

定义：由不同元素组成的集合，集合中是一组无序排列的可hash值，可以作为字典的key

1.不同元素组成

2.无序

3.集合中元素必须是不可变类型（数字，字符串，元组）

特性：集合的目的是讲不同的值放到一起，不同的集合间用来做关系运算，无需纠结于集合中单个值。

集合通过set(iterable)方法创建，参数iterable为可迭代对象。

s = set('hello')
print(s)  # 输出结果：{'l', 'o', 'e', 'h'}

s = set(['alex', 'alex', ''])
print(s)  # 输出结果：{'alex', '123'}

集合的方法

add(self,element) 添加方法

s = {1,2,3,4,5,6}
s.add('')
print(s)   #输出结果：{1, 2, 3, 4, 5, 6, '3'}

clear(self) 清空方法

s = {1,2,3,4,5,6}
s.clear()
print(s)   #输出结果：set()

copy(self) 拷贝/复制

s = {1,2,3,4,5,6}
s1 = s.copy()
print(s1)    #输出结果：{1, 2, 3, 4, 5, 6}

pop(self) 随机删除一个元素

s = {'s',1,2,3,4,5,6}
s.pop()
print(s)   #输出结果：{2, 3, 4, 's', 5, 6}

remove(self,element) 删除指定元素，如果给的元素不存在，那么删除会报错

s = {'ss',1,2,3,4,5,6}
s.remove('ss')
print(s)        #{1, 2, 3, 4, 5, 6}
s.remove('')
print(s)    #报错

discard(self,element) 删除指定元素，如果给的元素不存在，不会报错

s = {'ss',1,2,3,4,5,6}
s.discard('ss')
print(s)
s.discard('')
print(s)

---

python_l = ['','','']
linux_l = ['','','']

把上面的列表转换成集合 set

p_l = set(python_l)
l_l = set(linux_l)

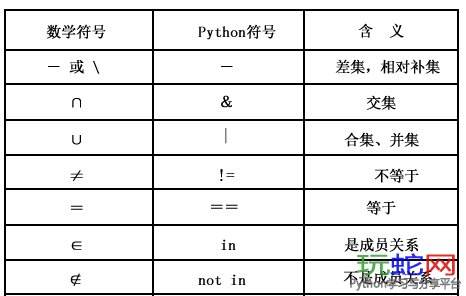
求交集intersection(self,s)

print(p_l.intersection(l_l))   #{'123', '456'}   求集合交集
print(p_l&l_l)      #符号法

求并集union(self,s)

print(p_l.union(l_l))   #{'456', '258', '789', '123'}
print(p_l|l_l)   # 符号法

求差集difference(self,s)

print("差集",p_l-l_l)
print(p_l.difference(l_l))

print("差集",l_l-p_l)
print(l_l.difference(p_l))

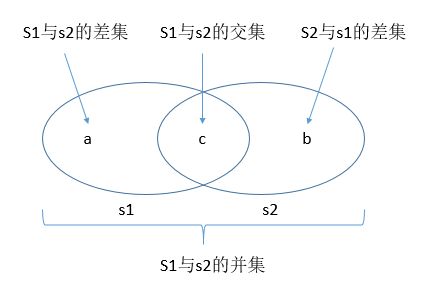
交叉补集

print(p_l.symmetric_difference(l_l))
print(p_l^l_l)     #符号法

difference_update()  求完差集之后更新下相关集合名词。
intersection_update()求完交集之后更新下相关集合名词。

isdisjoint(self,s) 求2个集合是否有公有部分，如果没有，返回True.

# s1 ={1,2}
# s2 ={3,5}
# s3 = s1.isdisjoint(s2)
# print(s3)  #True

issubset()方法用于判断集合的所有元素是否都包含在指定集合中，如果是则返回 True，否则返回 False。

s1={1,2}
s2 = {1,2,3}
print(s1.issubset(s2))  #s1是不是s2的子集
#s1<=s2 或者说 s1是s2的子集，s2是s2的父集

#issuperset(self,s)
print(s2.issuperset(s1)) #s2是不是s1的父集

update()按指定集合来更新,可以更新多个值， 区别于add()只能加一个值

s1 ={1,2}
s2 = {1,2,3}
s1.update(s2)
print(s1) # {1,2,3}

集合默认用set生成的是可变类型的，
frozenset 也可以生成不可变类型。 也就是没法使用pop  remover add等方法

# s=frozenset('hello')
# print(s)

列表去重复操作

names =['alex','alex','wupeiqi']
names = list(set(names))
print(names)