luogu3426 [POI2005]SZA-Template 后缀树

链接

bzoj不能auto

https://www.luogu.org/problemnew/show/P3426

思路

这个要求的串一定是S的前缀和S的后缀。

转化一下

建立出来fail树（fail[i]->i的树）

答案就在0和n之间的链条上，且答案在分界点上(上面全不可以，下面全可以)

这是样例的fail树



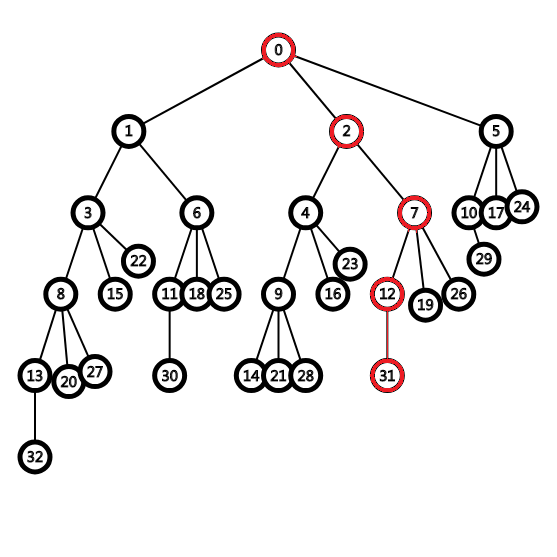
好了，我们从0到n挨着判断一下，n^2

其实满足条件就等价于我们选的这个前缀这个答案可以全部覆盖S串

就是说相邻的两个含有T的前缀串串的差<=|T|(这些串串一定在判断字符的子树内)

而且每次向下走的时候都要删除掉不是他子树内的点(因为他们不含有判定字符的前缀)

我们可以在删除的时候用链表维护子树内相邻的串的最大值

而且每个前缀只会被删一次，复杂度O(n)

错误

有点复杂度错误

bzoj不能auto、、、、

代码

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+7;
int n,fail[N],head=1,vis[N],ma=1;
char s[N];
vector<int> G[N];
struct node {int las,u,nxt;}e[N];
void del(int u) {
	if(vis[u]) return;
	e[e[u].las].nxt=e[u].nxt;
	e[e[u].nxt].las=e[u].las;
	if(e[e[u].nxt].u&&e[e[u].las].u)
		ma=max(ma,e[e[u].nxt].u-e[e[u].las].u);
//	for(auto v:G[u]) del(v);
//	for(int v=0;v<G[u].size();++v) del(v);
	for(vector<int>::iterator v=G[u].begin();v!=G[u].end();++v) del(*v);
}
void dfs(int u) {
	vis[u]=0;
    if(u>=ma) {printf("%d\n",u);exit(0);}
	del(u);
//	for(auto v:G[u])if(vis[v])dfs(v);
//	for(int v=0;v<G[u].size();++v) if(vis[v])dfs(v);
	for(vector<int>::iterator v=G[u].begin();v!=G[u].end();++v) if(vis[*v])dfs(*v);
}
int main() {
//    freopen("a.in","r",stdin);
//    freopen("a.out","w",stdout);
    scanf("%s",s+1);
    n=strlen(s+1);
    for(int i=2,p=0;i<=n;++i) {
        while(p>0&&s[i]!=s[p+1]) p=fail[p];
        if(s[i]==s[p+1]) p++;
        fail[i]=p;
    }
    for(int i=1;i<=n;++i) G[fail[i]].push_back(i),cout<<fail[i]<<" "<<i<<"\n";
    for(int p=n;p;p=fail[p]) vis[p]=1;
    for(int i=1;i<=n;++i) e[i].las=i-1,e[i].nxt=i+1,e[i].u=i;e[n].nxt=0;
    dfs(0);
    return 0;
}