poj 3683(2-SAT+SCC)

传送门:Problem 3683

https://www.cnblogs.com/violet-acmer/p/9769406.html

参考资料：

　　[1]:挑战程序设计竞赛

题意：

　　有n场婚礼，每场婚礼有起始时间si，结束时间ti，还有一个主持仪式需要花费ti时间，ti必须安排在婚礼的开始或者结束。

　　主持由神父来做，但是只有一个神父，所以各个婚礼的主持时间不能重复，不过神父可以在出席完一个主持仪式后，立刻出席另一个开始时间与其结束时间相等的主持仪式，问你有没有可能正常的安排主持时间，不能输出no，能的话要输出具体的答案：即每个婚礼的主持时间在那个时间段。

题解：

　　对于每个结婚仪式 i ，只有在开始或结束时进行主持仪式，两种选择，因此可定义变量 Xi;

　　　　　　Xi 为真 <=> 在开始时进行主持仪式

　　这样，对于婚礼 i 和 j ，如果Si~Si+Di 和 Sj~Sj+Dj 冲突，就有子句 (非Xi V 非Xj) 为真，对于开始和开始，开始和结束，结束和开始，结束和结束分别对应四条子句，也可得到类似的条件。

　　于是，要保证所有主持仪式的时间不冲突，只要考虑将这些所有的子句用 ^(合取)连接起来所得道德布尔公式就好了。

　　例如，对于输入的样例可以得到的布尔公式为：

　　　                                        　

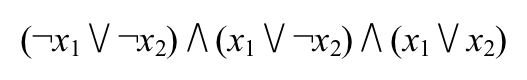
　　而当x1为真而x2为假时，其值为真。

　　这样，我们就把原问题转为了2-SAT问题，接下来只要进行强连通分量分解并判断是否有使得布尔公式值为真的一组布尔变量就好了。

　　以上分析来自挑战程序设计竞赛P326。

难点：　　

　　根据2-SAT建立有向图，用SCC分解强连通分量

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<vector>
 #include<cstring>
 #include<cmath>
 using namespace std;
 #define mem(a,b) (memset(a,b,sizeof a))
 #define pb push_back
 const int maxn=1e3+;

 //X1~Xn : 1~n
 //非X1~非Xn : n+1~2*n
 int n;
 int s[maxn];
 int t[maxn];
 int d[maxn];
 vector<int >G[*maxn],rG[*maxn];//注意此处是 2*maxn
 vector<int >vs;
 int scc[*maxn];
 bool vis[*maxn];
 void addEdge(int u,int v)
 {
     G[u].pb(v);
     rG[v].pb(u);
 }
 void SAT()
 {
     for(int i=;i <= n;++i)
     {
         for(int j=;j < i;++j)
         {
             if(max(s[i],s[j]) < min(s[j]+d[j],s[i]+d[i]))//第 i 场婚礼的开始时主持时间与第 j 场婚礼的开始时主持时间冲突
                 addEdge(i,j+n),addEdge(j,i+n);
             if(max(s[i],t[j]-d[j]) < min(t[j],s[i]+d[i]))//第 i 场婚礼的开始时主持时间与第 j 场婚礼的结束时主持时间冲突
                 addEdge(i,j),addEdge(j+n,i+n);//注意，第二处是 j+n -> i+n
             if(max(s[j],t[i]-d[i]) < min(t[i],s[j]+d[j]))//第 i 场婚礼的结束时主持时间与第 j 场婚礼的开始时主持时间冲突
                 addEdge(i,j),addEdge(i+n,j+n);//注意，第二处是 i+n -> j+n
             if(max(t[i]-d[i],t[j]-d[j]) < min(t[i],t[j]))//第 i 场婚礼的结束时主持时间与第 j 场婚礼的结束时主持时间冲突
                 addEdge(i+n,j),addEdge(j+n,i);
         }
     }
 }
 void Dfs(int u)
 {
     vis[u]=true;
     for(int i=;i < G[u].size();++i)
         if(!vis[G[u][i]])
             Dfs(G[u][i]);
     vs.pb(u);
 }
 void rDfs(int u,int k)
 {
     vis[u]=true;
     scc[u]=k;
     for(int i=;i < rG[u].size();++i)
     {
         int to=rG[u][i];
         if(!vis[to])
             rDfs(to,k);
     }
 }
 void SCC()
 {
     mem(vis,false);
     vs.clear();
     for(int i=;i <= n;++i)
         if(!vis[i])
             Dfs(i);
     mem(vis,false);
     int k=;
     for(int i=vs.size()-;i >= ;--i)
         if(!vis[vs[i]])
             rDfs(vs[i],++k);
 }
 void Init()
 {
     for(int i=;i < maxn;++i)
         G[i].clear(),rG[i].clear();
 }
 int main()
 {

     while(~scanf("%d",&n))
     {
         Init();
         for(int i=;i <= n;++i)
         {
             int h,m;
             char ch;
             scanf("%d%c%d",&h,&ch,&m);
             s[i]=h*+m;//将开始时间转化为分钟
             scanf("%d%c%d",&h,&ch,&m);
             t[i]=h*+m;//将结束时间转化为分钟
             scanf("%d",d+i);
         }
         SAT();//根据2-SAT建图
         SCC();//强连通分量分解
         bool flag=false;
         for(int i=;i <= n;++i)
             if(scc[i] == scc[i+n])
                 flag=true;
         if(flag)
             printf("NO\n");
         else
         {
             printf("YES\n");
             for(int i=;i <= n;++i)
             {
                 if(scc[i] > scc[i+n])
                     printf("%02d:%02d %02d:%02d\n",s[i]/,s[i]%,(s[i]+d[i])/,(s[i]+d[i])%);
                 else
                     printf("%02d:%02d %02d:%02d\n",(t[i]-d[i])/,(t[i]-d[i])%,t[i]/,t[i]%);
             }
         }
     }
     return ;
 }