c++实现排序（简单插入，希尔，选择，快速，冒泡，堆排）

简单插入排序

适用于记录较少且基本有序的记录。算法思想：给定一个存在分界线的序列，分界线左边有序，右边无序，依次将右边的没排序的数与左边序列进行比较，插入相应位置，再对分界线做出相应调整，下面用图来说明。

代码如下：

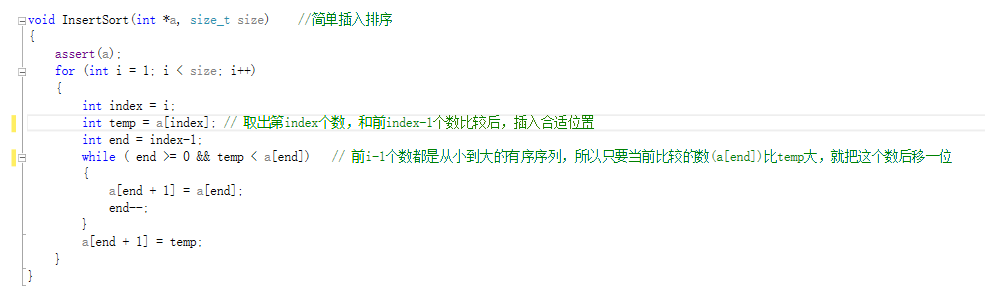
时间复杂度：最好情况O(n),最坏O(n^2)。

希尔排序

希尔排序是改进后的简单插入排序。算法思想：将序列分组排序，最后在进行一次简单插入排序。

至于如何分组，下面我将用图向大家展示

这些数的下标从0开始，即0，3 ，6，9为一组，1，4，7为一组，2，5，8为一组。也就是gap%3下标相等的为一组。gap=gap/3+1.

代码如下：

void ShellSort(int *a, size_t size)    //希尔排序
{
  assert(a);
  int gap = size;
  while (gap > 1)
  {
      gap = gap / 3 + 1;
      for (int i = gap; i < size; ++i)
     {
     　　int index = i;
     　　int tem = a[index];
    　　 int end = index - gap;
     　　while (end >= 0 && tem < a[end])
     　　{
     　　　　 a[end + gap] = a[end];
      　　　　end -= gap;
     　　}
    　　 a[end + gap] = tem;
     }
  }
}

时间复杂度为O(n^1.5)

选择排序

算法思想：每次循环找到最小值，并交换。

代码如下：

void SelectSort(int *a, size_t size)
{
 　　assert(a);
 　　for (int i = 0; i < size; ++i)
 　　{
 　　　　 int minindex = i;
 　　　　 int tem;
  　　　　for (int j = i + 1; j < size; ++j)
  　　　　{
  　　　　　　 if (a[j] < a[minindex])
  　　　　　　 {
   　　　　　　　　 minindex = j;
    　　　　　　　　tem = a[minindex];
   　　　　　　　　 a[minindex] = a[i];
   　　　　　　　　 a[i] = tem;
   　　　　　　}
 　　　　 }
 　　}
}

时间复杂度O(n^2)

快速排序

算法思想：选取key，将key调整到一个合理的位置，使得左边全部小于key，右边全部大于key；

如何将key调整到合适位置，这里用到三数取中的方法。

注意：如果序列基本有序或序列个数较少，则可以采用简单插入排序，因为快速排序对于这些情况效率不高；

代码如下：

int GetMidIndex(int *a, int left, int right)     /////////三数取中/////////
{
 　　assert(a);
　　 int mid=left+(right-left)/2;
 　　if (left < right)
　　 {
  　　　　if (a[mid] < a[left])
   　　　　　　return left;
 　　　　 else if (a[mid] < a[right])
  　　　　　　 return mid;
 　　　　 else
   　　　　　　return right;
 　　}
 　　else
 　　{
 　　　　 if (a[mid] < a[right])
  　　　　　　 return right;
  　　　　else if (a[mid] < a[left])
   　　　　　　return mid;
  　　　　else
  　　　　　　 return left;
　　 }
}

int PartionSort(int *a, int left, int right)
{
 　　int midIndex = GetMidIndex(a, left, right);
 　　swap(a[midIndex], a[right]);
 　　int cur = left;
 　　int prev = left - 1;
　　 while (cur < right)
 　　{
 　　　　 if (a[cur] < a[right] && ++prev != cur)
 　　　　 {
   　　　　　　swap(a[cur], a[prev]);
  　　　　}
  　　　　++cur;
 　　}
 　　++prev;
 　　swap(a[prev], a[right]);
　　 return prev;
}

void QuickSort(int *a,int left,int right)
{
 　　assert(a);
 　　int size = right - left + 1;
 　　if (right - left > 13)        //////////优化：当长度大于13时采用快排，小于13则退化为简单插入排序////////////
 　　{
  　　　　int boundary = PartionSort(a, left, right);
 　　　　 QuickSort(a, left, boundary - 1);
  　　　　QuickSort(a, boundary + 1, right);
　　 }
 　　else
 　　　　 InsertSort(a, size);   /////简单插入排序
}

冒泡排序

算法思想：两两比较再交换，一趟排序下来只能找到一个最大，其余都是乱序，再重复这样做就可以按照从小到大的顺序排下来。

代码如下：

void BubbleSort(int *a, size_t size)
{
 　　assert(a); 
 　　for (int i = 0; i < size; i++)
 　　{
  　　　　for (int j = 0; j = size - 1 - i; j++)
  　　　　{
  　　　　　　 if (a[j] > a[j + 1])
   　　　　　　{
   　　　　　　　　 int tem = a[j + 1];
   　　　　　　　　 a[j + 1] = a[j];
    　　　　　　　　a[j] = tem;
  　　　　　　 }
  　　　　}
 　　}
}

以上冒泡排序有一个效率问题，当序列基本接近有序时，则不需要进行排序，以上代码则会进行不断的比较，影响效率，因此做以下改进，设一个布尔型变量flag,

如果一次循环中没有交换过元素，则说明已经排好序.

优化：

void BubbleSort(int *a, size_t size)
{
 　　assert(a);

bool flag=true;
 　　for (int i = 0; i < size; i++)
 　　{

　　　　  bool flag=false;
  　　　　for (int j = 0; j = size - 1 - i; j++)
  　　　　{
  　　　　　　 if (a[j] > a[j + 1])
   　　　　　　{
   　　　　　　　　 int tem = a[j + 1];
   　　　　　　　　 a[j + 1] = a[j];
    　　　　　　　　a[j] = tem;

　　　　　　　　　 bool flag=true;
  　　　　　　 }
  　　　　}
 　　}
}

堆排序

算法思想：将待排序列建成大堆，再将堆顶数据与堆的最后一个叶子节点的数据交换，再重新调整为大堆，每次堆的数据个数减1。

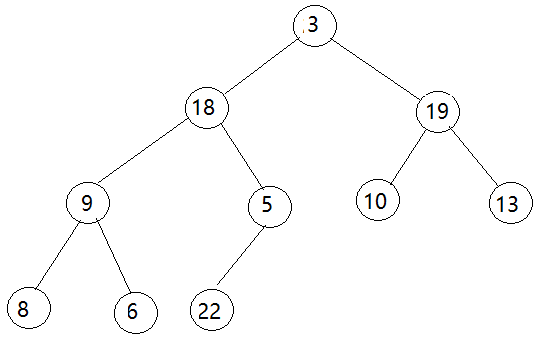
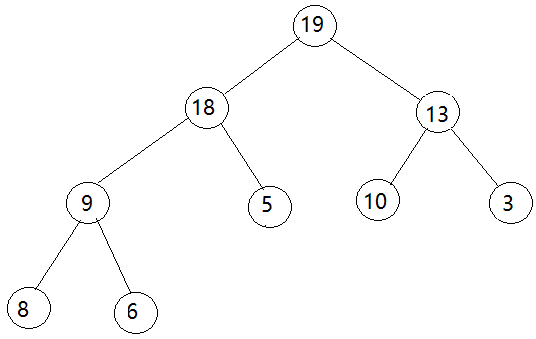
依次类推......

代码如下：

void HeapSort(int *a, size_t size)    //堆排序
{
　　 assert(a);
　　 for (int i = (size - 2) / 2; i >= 0; --i)
 　　{
 　　　　 Adjustdown(a, size, i);
 　　}
　　 for (int i = 0; i < size; ++i)
 　　{
 　　　　 swap(a[0], a[size - i - 1]);
  　　　　Adjustdown(a, size - i - 1, 0);
 　　}
}

/////////建大堆/////////

void Adjustdown(int *a, size_t size, int root)
{
 　　int child = 2 * root + 1;
　　 while (child < size)
 　　{
 　　　　 if (child + 1 < size && a[child + 1] > a[child])
  　　     {
   　　　　　　++child;
  　　　　}
 　　　　 if (a[child]>a[root])
  　　　　{
   　　　　　　swap(a[child], a[root]);
 　　　　　　  root = child;
   　　　　　　child = 2 * root + 1;
  　　　　}
  　　　　else
 　　　　 {
 　　　　　　 break;
 　　　　 }
 　　}
}