【暑假培训1】test1

T1：

30pts：直接暴力三层循环枚举

就就就先不写代码了qwq；

70pts：

因为X+Y+Z==0

所以我们可以考虑枚举X和Y，然后利用↑式子求出Z=-X-Y；

然后touli xcg的70pts code：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<set>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int t,n,x,tot,ans;
int a[];
set<int> st;
int main()
{
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    t=read();
    while(t--)
    {
        ans=;tot=;
        st.clear();
        n=read();
        for(int i=;i<=n;i++)
        {
            x=read();
            st.insert(x);
        }
        set<int>::iterator it;    //定义前向迭代器
        for(it=st.begin();it!=st.end();it++)
        {
            a[++tot]=*it;
            //cout<<a[tot]<<' ';
        }
        if(tot<)
        {
            printf("0\n");
            continue;
        }
        for(int i=;i<=tot;i++)           //作为相反数组的第一个数
        {
            if(a[i]>=) break;
            for(int j=i+;j<=tot;j++)     //第二个数
            {
                for(int k=j+;k<=tot;k++) //第三个数
                {
                    if(a[k]<=) continue;
                    if(a[i]+a[j]+a[k]==)
                    {
                        ans++;
                        break;
                    }
                }
            }
        }
        printf("%d\n",ans);
    }
    return ;
}

70pts Code

100pts：

SOLUTION：

这里对于我们枚举的j和k，我们会发现有很大一部分是浪费了的，当我们排序过后，如果相加的和<0时，我们增大j，当相加>0时，我们令最大的k--；（因为k是从最后开始枚举，所以如果连k和其他两数相加都不能满足和>0，显然我们要使j增大）

然后unique去重；

以下是STD：

#include <cstdio>
#include <algorithm>
const int numsize = ;

int T, N;
int a[numsize];
inline int getint() {
    register int num = ;
    register char ch = , last;
    do last = ch, ch = getchar(); while (ch < '' || ch > '');
    do num = num *  + ch - '', ch = getchar(); while (ch >= '' && ch <= '');
    if (last == '-') num = -num;
    return num;
}

int main() {
    freopen("sum.in", "r", stdin);
    freopen("sum.out", "w", stdout);
    T = getint();
    for (int i = ; i < T; i++) {
        N = getint();
        for (int i = ; i <= N; i++)
            a[i] = getint();
        std::sort(a + , a + N + );
        int cnt = ;
        N = std::unique(a + , a + N + ) - (a + );
        for (int i = ; i < N; i++) {
            int left = i + , right = N;
            while (left < right) {
                if (a[i] + a[left] + a[right] == ) {
                    left++;
                    cnt++;
                }
                if (a[i] + a[left] + a[right] > ) right--;
                if (a[i] + a[left] + a[right] < ) left++;
            }
        }
        printf("%d\n", cnt);
    }
    return ;
}

还有一个我的code，然后用70pts思路过了100%数据就很迷了？？？

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<set>

#define ll long long

using namespace std;

inline ll read(){
    ll ans=;
    char last=' ',ch=getchar();
    while(ch>''||ch<'') last=ch,ch=getchar();
    while(ch<=''&&ch>='') ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return  ans;
}
bool cmp(int x,int y){return x<y;}

ll n,ans;
ll c[],fcnt,zcnt,cnt0;
bool bj0;

ll find(ll x){
    int l=,r=n;
    int mid;
    while(l<=r){
        mid=l+r>>;
        if(c[mid]>x) r=mid-;
        else l=mid+;
    }
    if(c[r]!=x) return ;
    return ;
}

void solve(){
    sort(c+,c+n+,cmp);
    ll sum;
    for(int i=;i<=n;i++){
        if(c[i]==c[i-]) continue;
        for(int j=i+;j<=n;j++){
            if(c[i]==c[j]||c[j]==c[j-]) continue;
            sum=c[i]+c[j];
            if(-sum<=c[i]||-sum<=c[j]) continue;
            if(sum==&&bj0==){
                ans++;
                continue;
            }
            ans+=find(-sum);
        }
    }
}

int main(){
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    int T;
    scanf("%d",&T);
    for(int i=;i<=T;i++){
        n=read();
        if(n<){
            printf("0\n");
            continue;
        }
        bool bjf=,bjz=;
        memset(c,,sizeof(c));
        cnt0=;bj0=;ans=;
        for(int j=;j<=n;j++){
            ll _num=read();
            if(_num<) bjf=,c[j]=_num;
            if(_num>) bjz=,c[j]=_num;
            if(_num==) bj0=;
        }
        if(bjf==||bjz==) {
            printf("0\n");
            continue;
        }
        solve();
        printf("%lld\n",ans);
    }

    return ;
}

T2：

看数据范围p<=2*10^6，奇怪？那么我们大胆猜想gi一定<=2*10^6那一定会有gj==gi

那么我们找循环节

两个数组f和g，f数组记录我们所计算的函数值，然后g数组记录这个值第一次出现在哪里。

然后从第二项开始计算，直到计算到n，然后写一个朴素的函数，计算。然后如果我们找到了一个数，之前已经出现过了，那么我们记这个数为循环点，然后弹出；否则记g[f[i]]=i；

然后如果我们还没有找到循环节，就直接输出就可以了；

如果找到循环点了，我们可以令m=第一循环结最前所在项数-1，l=第二个循环的第一个点项数-第一循环结最前点所在项数；

然后先令n-=m；（把不循环的部分减掉）

然后将剩下循环的部分%=l；这样剩下的就是不足一个循环结的问题；

当n==0时，为循环节最后一个，因此令n=l；然后输出f[m+n]；

STD：

#include <cstdio>
#include <cstring>
const int mod = ;

int F(long long x, int a, int b, int c, int p) {
    long long ans = ;
    ans = a * x % p * x % p;
    ans = (ans + b * x % p) % p;
    ans = (ans + c) % p;
    return ans;
}

int g1, a, b, c, p;
long long n;
int f[mod];
int g[mod];

int main() {
    freopen("sequence.in", "r", stdin);
    freopen("sequence.out", "w", stdout);
    scanf("%d %d %d %d %lld %d", &g1, &a, &b, &c, &n, &p);
    g1 = (g1 % p + p) % p;
    a = (a % p + p) % p;
    b = (b % p + p) % p;
    c = (c % p + p) % p;
    //先处理成正数
    memset(g, , sizeof(g));
    f[] = g1, g[g1] = ;
    int point = ;
    for (int i = ; true; i++) {
        if (i > n) break;
        f[i] = F(f[i - ], a, b, c, p);
        if (g[f[i]]) {
            point = i;
            break;
        }
        g[f[i]] = i;
    }
    if (!point)
        printf("%d\n", f[n]);
    else {
        int m = g[f[point]] - , l = point - g[f[point]];
        n -= m;
        n %= l;
        if (n == ) n = l;
        printf("%d\n", f[m+n]);
    }

    return ;
}

T3：

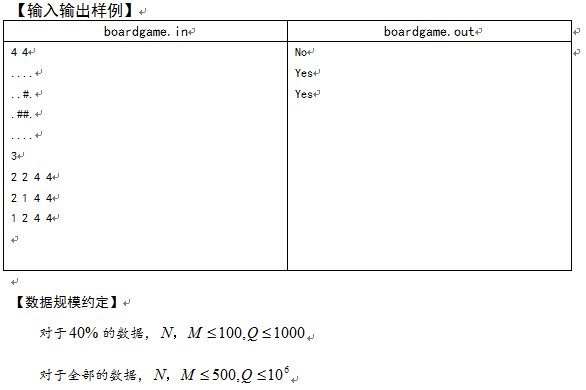
考虑整体分治：

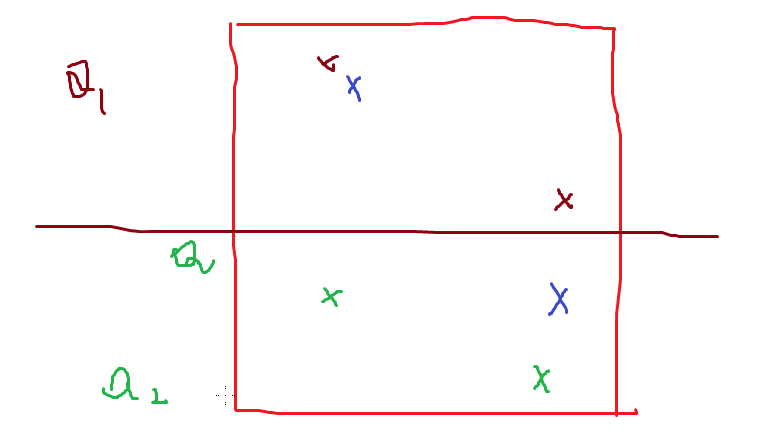
考虑三种情况，一种全在p行之上，一种全在p行之下，还有一种一个在p之上，一个在p之下；

对于全在p行之上和全在p行之下的情况，我们可以直接递归的解决，只需要解决一个在p行之上，一个在p行之下的问题：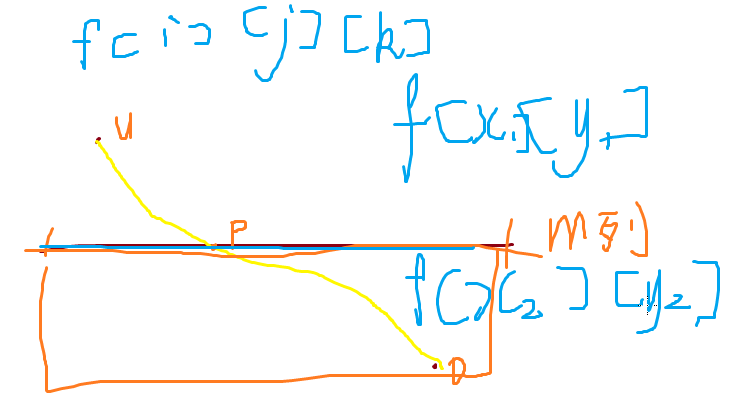

处理01数组处理每个点到第k列的每一点是否可以走到（1为可以，0不可以）然后比较是否有相同

预处理：

凹凸不平：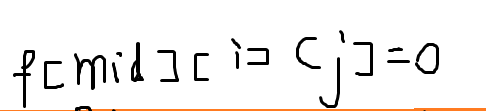

否则记为：

上面乱七八糟的qwq，还是下面比较清晰：

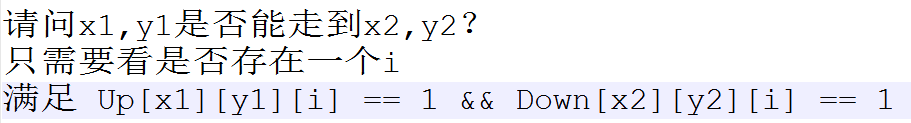
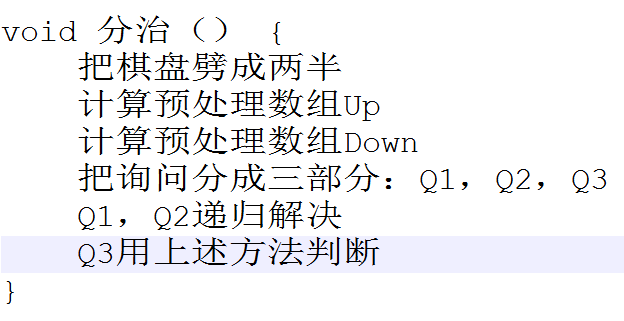
Up的计算

Up往右走能否走通+往下走能否走通，二者满足其一即可：

Down同理

然后如果只存1/0，会爆炸，因此我们压个位。

比如直接让101011存成一个int43

把32位01数组压成一个int/64位long long数组

#include <cstdio>
#include <vector>
#include <bitset>
using std::vector;
using std::bitset;
const int QUERY_SIZE = ;
const int MAP_SIZE = ;

int N, M, Q;
char map[MAP_SIZE][MAP_SIZE];
int ans[QUERY_SIZE];
bitset<MAP_SIZE> up[MAP_SIZE][MAP_SIZE], down[MAP_SIZE][MAP_SIZE];
struct query {
    int x1, y1, x2, y2, id;
};

query q;
void solve(vector<query> v, int l, int r) {
    int m = (l + r) >> ;
    if (l > r) return ;
    for (int i = m; i >= l; i--)
        for (int j = M; j >= ; j--) {
            up[i][j] = ;
            if (map[i][j] == '.') {
                if (i == m) up[i][j].set(j);
                else up[i][j] |= up[i + ][j];
                if (j != M) up[i][j] |= up[i][j + ];
            }
        }
    for (int i = m; i <= r; i++)
        for (int j = ; j <= M; j++) {
            down[i][j] = ;
            if (map[i][j] == '.') {
                if (i == m) down[i][j].set(j);
                else down[i][j] |= down[i - ][j];
                if (j != ) down[i][j] |= down[i][j - ];
            }
        }
    vector<query> vl, vr;
    for (vector<query>::iterator it = v.begin(); it != v.end(); it++) {
        q = *it;
        if (q.x2 < m) vl.push_back(q);
        else if (q.x1 > m) vr.push_back(q);
        else ans[q.id] = (up[q.x1][q.y1] & down[q.x2][q.y2]).any();
    }
    solve(vl, l, m - );
    solve(vr, m + , r);
}

int main() {
    freopen("boardgame.in", "r", stdin);
    freopen("boardgame.out", "w", stdout);
    scanf("%d %d", &N, &M);
    for (int i = ; i <= N; i++)
        scanf("%s", map[i] + );
    vector<query> v;
    scanf("%d", &Q);
    for (int i = ; i < Q; i++) {
        scanf("%d %d %d %d", &q.x1, &q.y1, &q.x2, &q.y2);
        q.id = i;
        v.push_back(q);
    }
    solve(v, , N);
    for (int i = ; i < Q; i++)
        puts(ans[i] ? "Yes" : "No");
    return ;
}