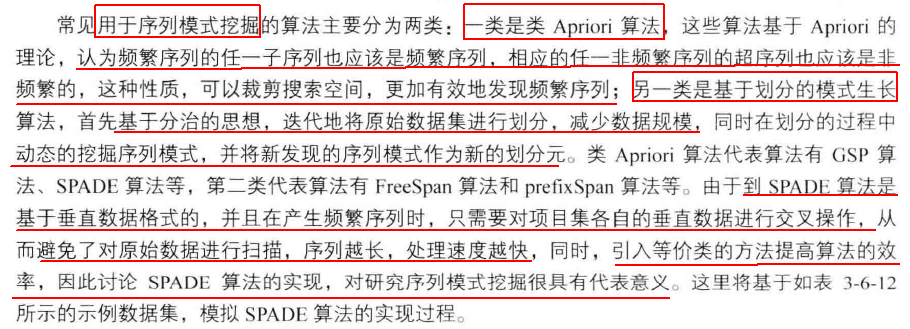
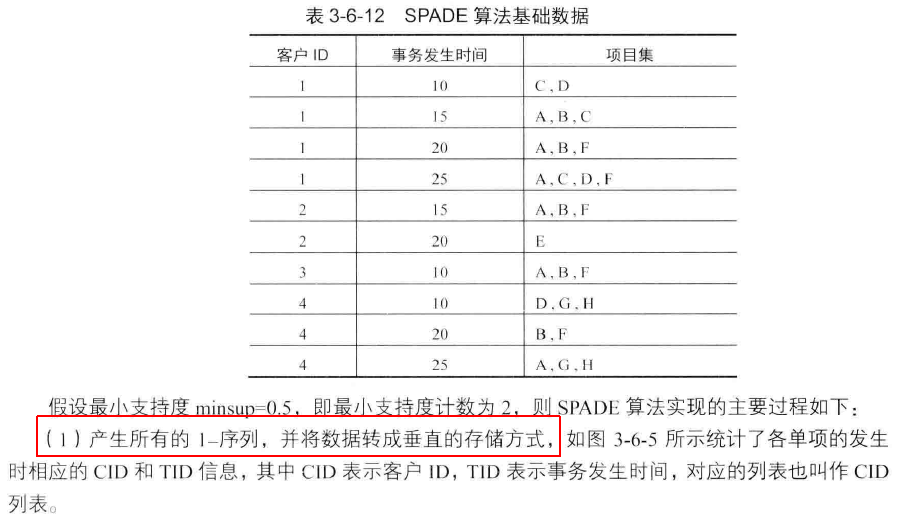
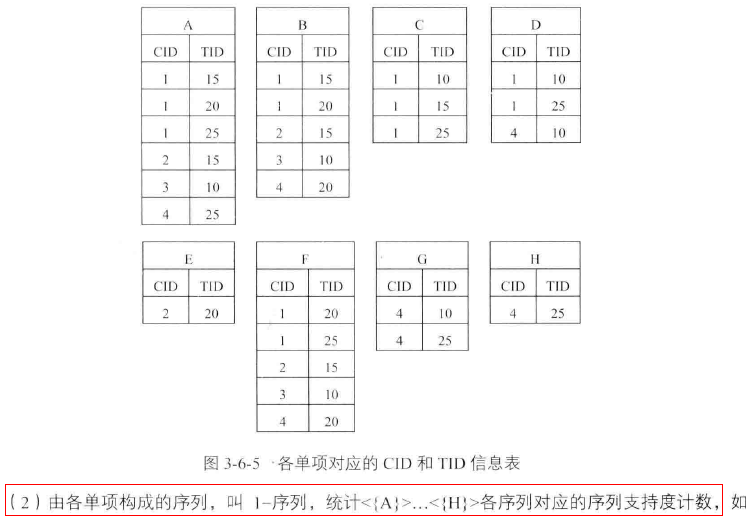
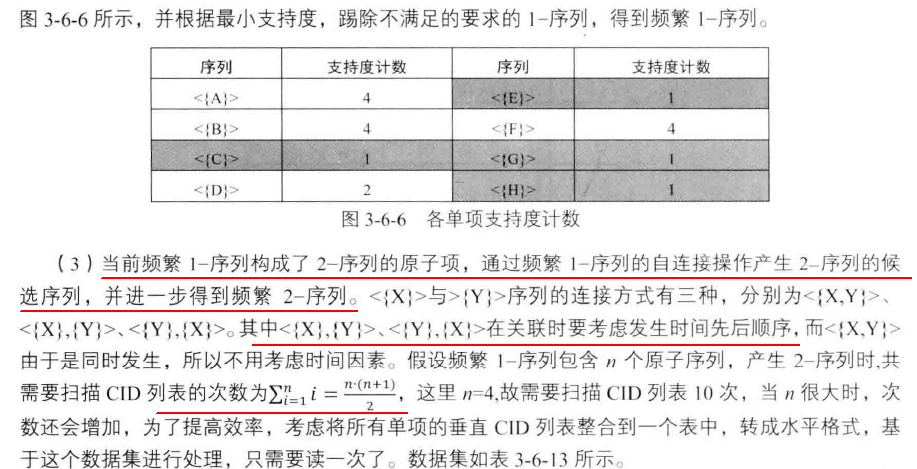
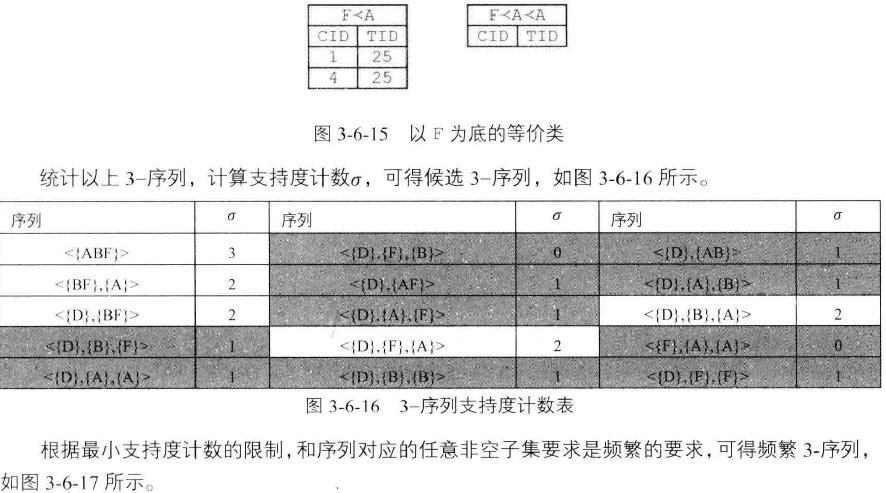
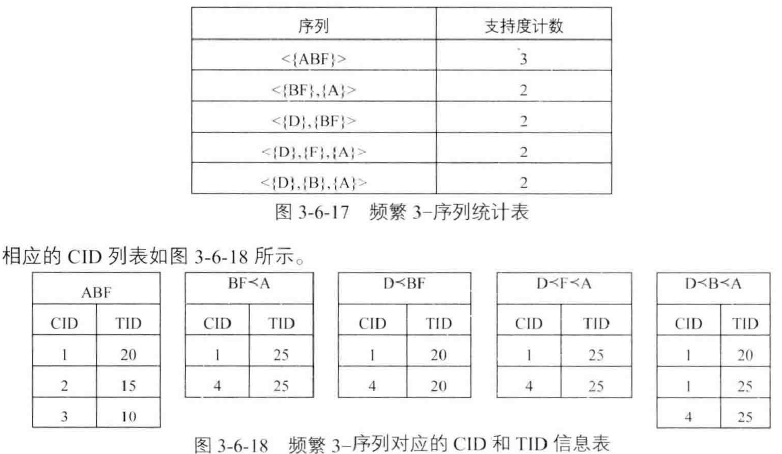
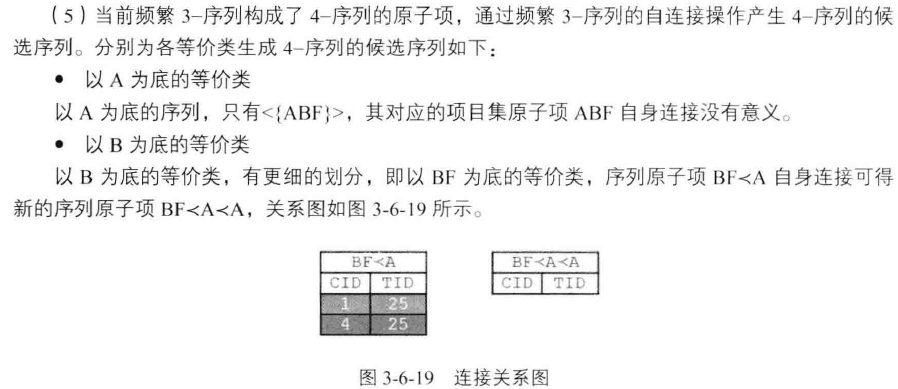
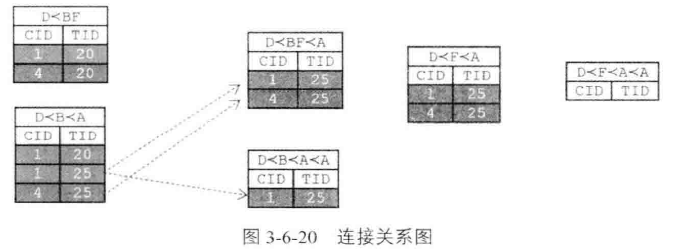
序列模式挖掘--SPADE算法



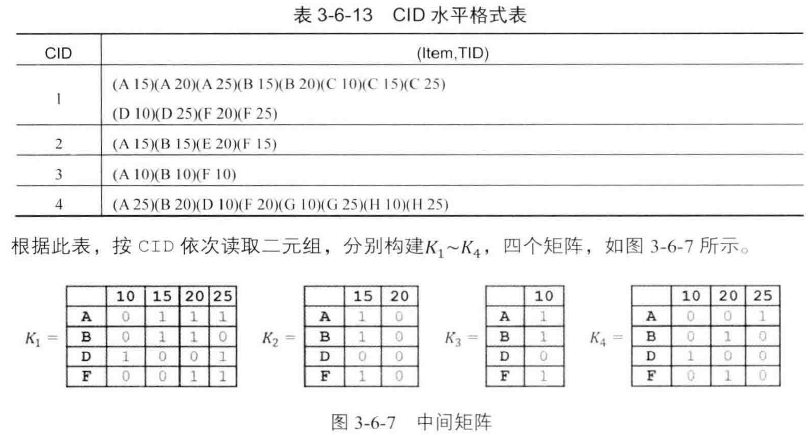


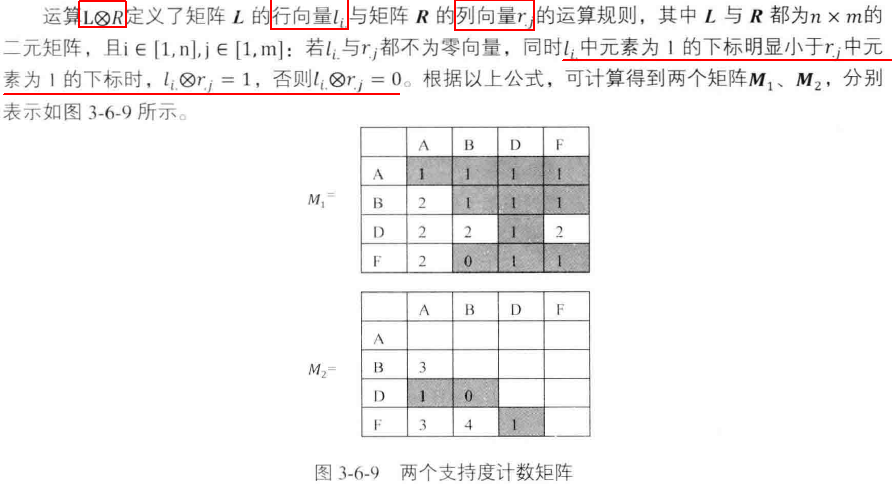




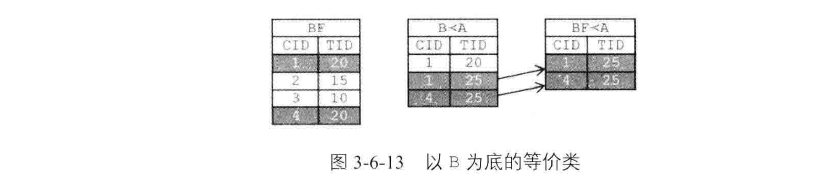
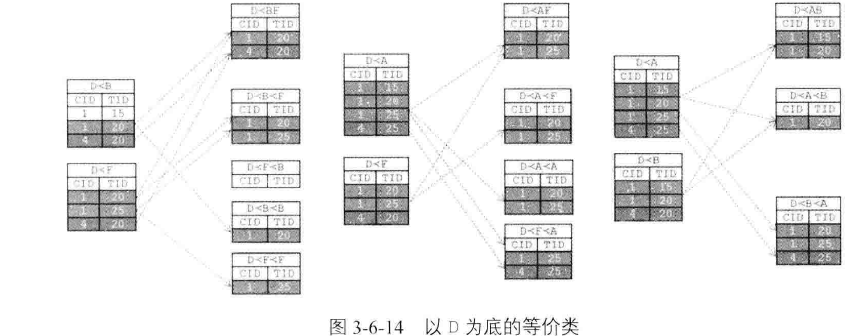




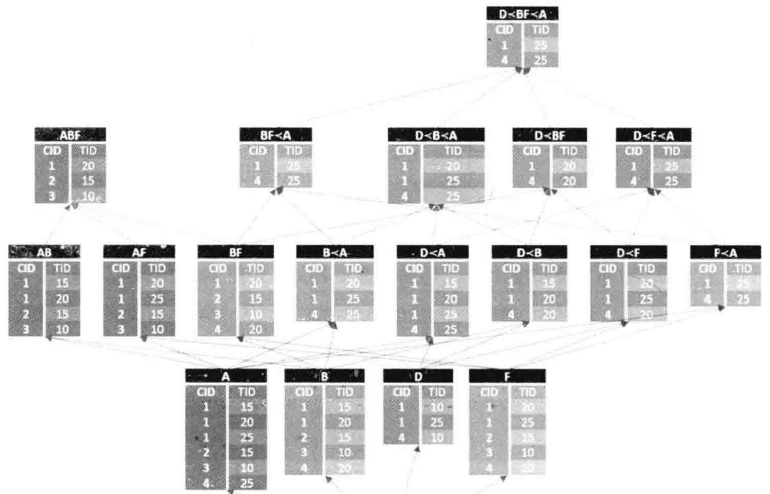


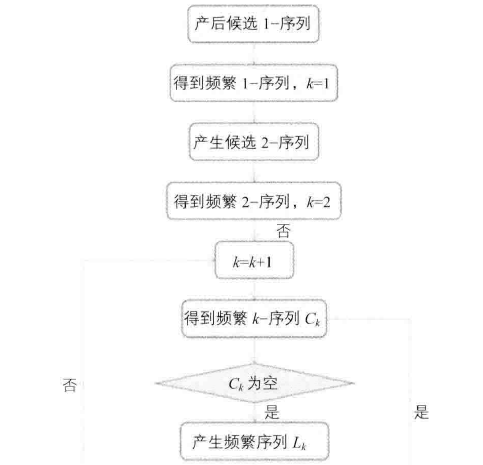
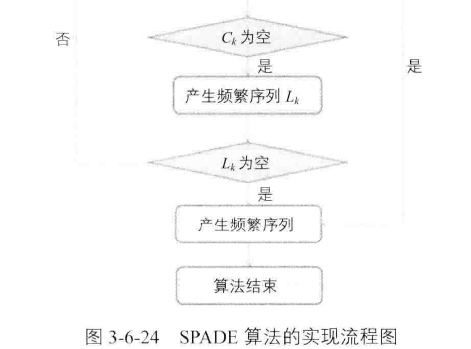
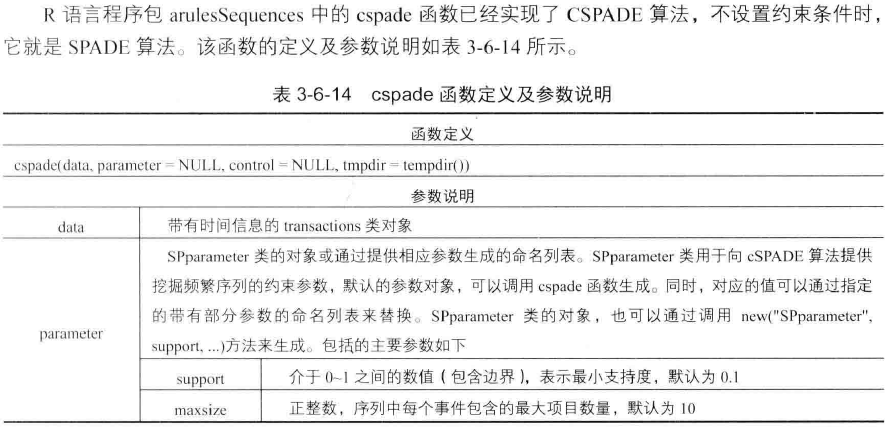
序列模式挖掘--SPADE算法的更多相关文章
- 数据挖掘进阶之序列模式挖掘GSP算法
数据挖掘进阶之序列模式挖掘GSP算法 绪 继续数据挖掘方面算法的讲解,前面讲解了数据挖掘中关联规则算法FP-Growth的实现.此篇博文主要讲解基于有趣性度量标准的GSP序列模式挖掘算法.有关论文后期 ...
- gsp序列模式挖掘
数据挖掘进阶之序列模式挖掘GSP算法 绪 继续数据挖掘方面算法的讲解,前面讲解了数据挖掘中关联规则算法FP-Growth的实现.此篇博文主要讲解基于有趣性度量标准的GSP序列模式挖掘算法.有关论文后期 ...
- 数据挖掘进阶之关联规则挖掘FP-Growth算法
数据挖掘进阶之关联规则挖掘FP-Growth算法 绪 近期在写论文方面涉及到了数据挖掘,需要通过数据挖掘方法实现软件与用户间交互模式的获取.分析与分类研究.主要涉及到关联规则与序列模式挖掘两块.关联规 ...
- 增量关联规则挖掘—FUP算法
一.背景介绍 关联规则( Association rule)概念最初由Agrawal提出,是数据挖掘的一个重要研究领域, 其目的是发现数据集中有用的频繁模式. 静态关联规则挖掘,是在固定数据集和支持度 ...
- 频繁模式挖掘apriori算法介绍及Java实现
频繁模式是频繁地出如今数据集中的模式(如项集.子序列或者子结构).比如.频繁地同一时候出如今交易数据集中的商品(如牛奶和面包)的集合是频繁项集. 一些基本概念 支持度:support(A=>B) ...
- 海量数据挖掘MMDS week2: 频繁项集挖掘 Apriori算法的改进:非hash方法
http://blog.csdn.net/pipisorry/article/details/48914067 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- 海量数据挖掘MMDS week2: 频繁项集挖掘 Apriori算法的改进:基于hash的方法
http://blog.csdn.net/pipisorry/article/details/48901217 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- 推荐系统第4周--- 基于频繁模式的推荐系统和关联规则挖掘Apriori算法
数据挖掘:关联规则挖掘
- [数据挖掘课程笔记]关联规则挖掘 - Apriori算法
两种度量: 支持度(support) support(A→B) = count(AUB)/N (N是数据库中记录的条数) 自信度(confidence)confidence(A→B) = count ...
随机推荐
- springdata的jpa配置文件application.xml
<?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.spr ...
- SqlServer中插入数据后如何得到主键ID
使用@@IDENTITY 例如:insert into student(name,age) values('fanqi',23) select @@identity 使用 OUTPUT inserte ...
- jsp文件
新建的jsp文件比新建的html文件多了一行内容<%@ page contentType="text/html; charset=utf-8" %>,这样不会显示乱码 ...
- const和static const的区别(未整理)
对于C/C++语言来讲,const就是只读的意思,只在声明中使用;static一般有2个作用,规定作用域和存储方式.对于局部变量,static规定其为静态存储方式,每次调用的初始值为上一次调用的值,调 ...
- RPC 框架 介绍 (转)
出处: 谁能用通俗的语言解释一下什么是 RPC 框架? 知乎: 问题:了解到最近 Java 的 Netty 很火,只知道它是这样类型的一种框架.想了解一下它主要用于解决了什么问题?适用于什么样的场景? ...
- 数据库oracle一些操作(MiTAC)
oracle计算时间差函数: 两个Date类型字段:START_DATE,END_DATE,计算这两个日期的时间差(分别以天,小时,分钟,秒,毫秒): 天: ROUND(TO_NUMBER(END_D ...
- @RequestMapping-限定参数映射
限定参数映射 测试:
- Vue报错:Property or method "XXX" is not defined on the instance but referenced during render. Make sure that this property is reactive...
在Vue中定义方法或者属性时,因为粗心疏忽可以能会报该错误 [Vue warn]: Property or method "search" is not defined on th ...
- 第七篇 CSS盒子
CSS盒子模型 在页面上,我们要控制元素的位置,比如:写作文一样,开头的两个字会空两个格子(这是在学校语文作文一样),其后就不会空出来,还有,一段文字后面跟着一张图,它们距离太近,不好看,我们要移 ...
- Python内置函数清单
作者:Vamei 出处:http://www.cnblogs.com/vamei Python内置(built-in)函数随着python解释器的运行而创建.在Python的程序中,你可以随时调用这些 ...
