6359. 【NOIP2019模拟2019.9.15】小ω的树(tree)（定期重构）

题目描述

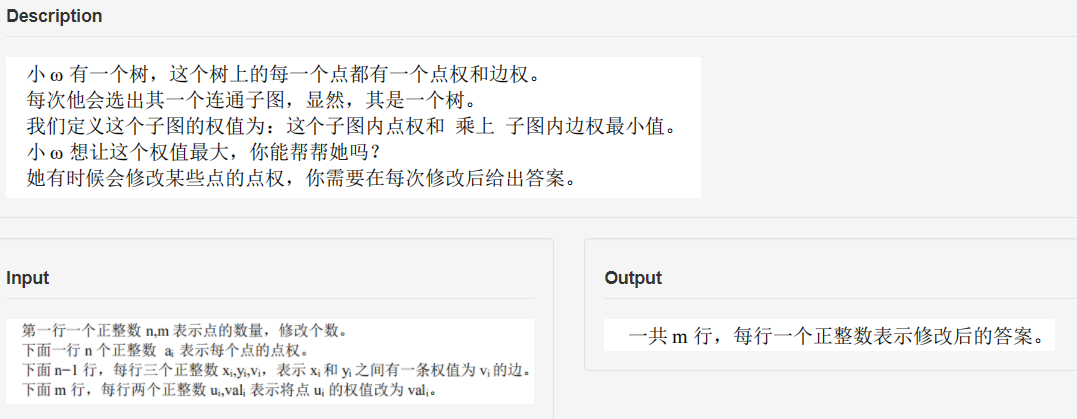
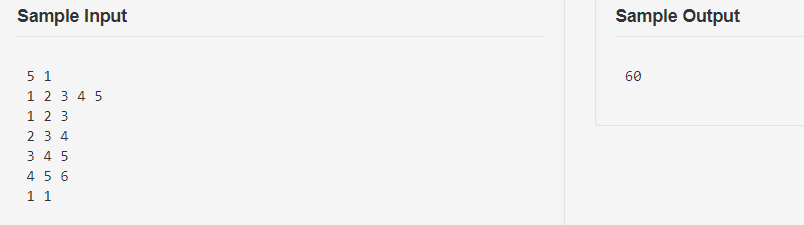
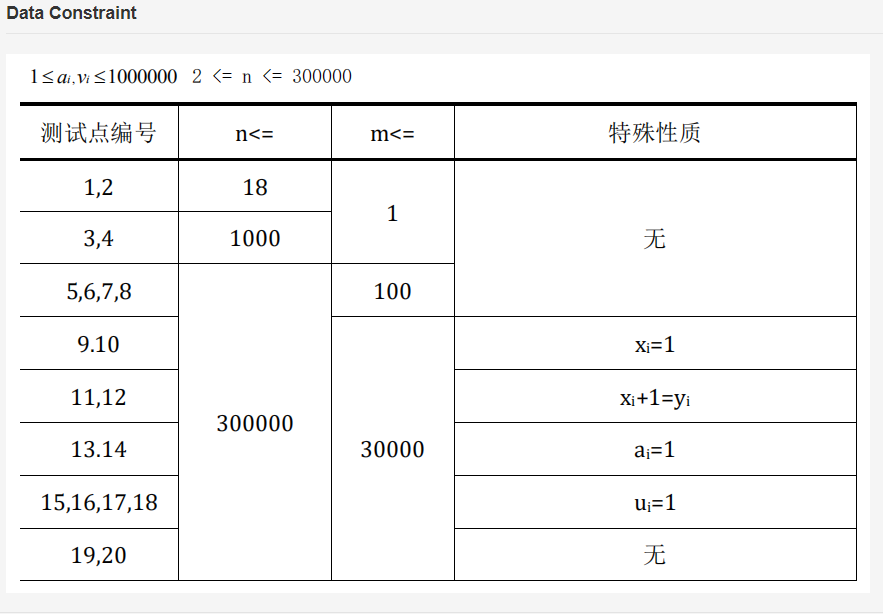
题解

qy的毒瘤题

CSP搞这种码农题当场手撕出题人

先按照边权从大到小建重构树，然后40%暴力修改+查找即可

100%可以定期重构+平衡规划，每次把B个询问拉出来建虚树，在虚树上暴力维护每一段的凸壳，在凸壳上二分

虚树建法：

按照dfs序排序，每次用栈维护从根到当前点的栈

每次把当前点和栈顶做lca，若lca=栈顶就直接加，否则一直弹到栈顶是lca的祖先，顺便记录下每个点在虚树上的父亲

如果栈顶=之前的lca就不用管，否则加上lca，修改最后弹出的点的父亲

（注意要把根加进去）

---

设每次搞B个询问，那么时间为\(O(QB\log n+\frac{Qn}{B})\)，极限数据下函数长这样：

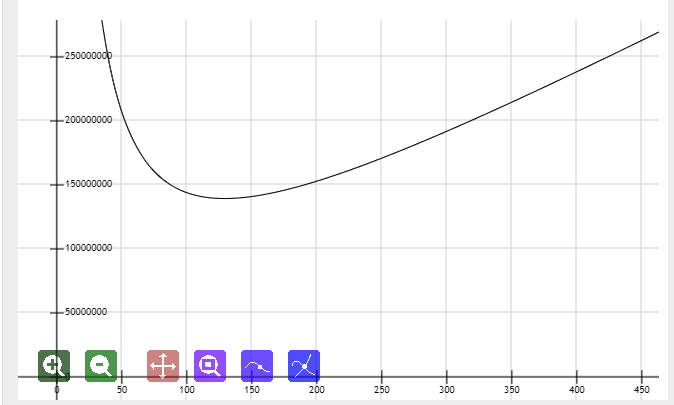
可以看出，实际最优的B为\(\sqrt{\frac{n}{\log n}}\)，但由于常数等原因这样取会被卡成SB

所以B取\(\sqrt{n}\)就可以过了（

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define inc(x,y) (bg[x]<=bg[y] && ed[y]<=ed[x])
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;

struct type{
	int x,y,s;
} b[300001];
struct Type{
	int x,s,id;
} A[30001];
int c[600001];
int C[2001];
long long d[600001][2];
double dx[600001];
int l2[600001];
int r2[600001];
int w[600001];
int v[600001]; //bian
long long sum[600001];
int fa[600001][20];
int fa2[600001];
int son[600001][2];
int bg[600001];
int ed[600001];
int D[600001];
int Fa[600001];
long long ans[30001];
bool bz[600001];
int p[2001];
long long X[600001];
long long ANS[600001];
int d2[600001][2];
bool Bz[600001];
int n,Q,B,i,j,k,l,N,L,R,T,I,tot;
long long Ans,S;

bool cmp(type a,type b)
{
	return a.s>b.s;
}
bool Cmp(Type a,Type b)
{
	return bg[a.x]<bg[b.x];
}
bool Cmp2(Type a,Type b)
{
	return a.id<b.id;
}

int gf(int t)
{
	int i,t2;

	t2=0;
	while (Fa[t]!=t)
	{
		d2[++t2][0]=t;
		t=Fa[t];
	}
	fo(i,1,t2)
	Fa[d2[i][0]]=t;

	return t;
}

void dfs()
{
	int i,j,k,l,T,t2;

	t2=1;
	d2[1][0]=N;
	d2[1][1]=0;
	while (t2)
	{
		T=t2;

		if (!d2[t2][1])
		{
			D[d2[t2][0]]=D[fa[d2[t2][0]][0]]+1;
			bg[d2[t2][0]]=++j;

			fo(i,1,19)
			fa[d2[t2][0]][i]=fa[fa[d2[t2][0]][i-1]][i-1];
		}
		if (d2[t2][1]<=1)
		{
			if (son[d2[t2][0]][d2[t2][1]])
			{
				++t2;
				d2[t2][0]=son[d2[T][0]][d2[T][1]];
				d2[t2][1]=0;
			}

			++d2[T][1];
		}
		else
		{
			ed[d2[t2][0]]=j;
			--t2;
		}
	}
}

void swap(int &x,int &y)
{
	int z=x;
	x=y;
	y=z;
}

int lca(int x,int y)
{
	int i;

	if (D[x]<D[y]) swap(x,y);

	fd(i,19,0)
	if (D[fa[x][i]]>=D[y])
	x=fa[x][i];

	fd(i,19,0)
	if (fa[x][i]!=fa[y][i])
	{
		x=fa[x][i];
		y=fa[y][i];
	}

	if (x!=y) x=fa[x][0];
	return x;
}

void init()
{
	int i,j,k,l;

	scanf("%d%d",&n,&Q);//B=floor(sqrt((n+n)/(log(n)/log(2)+1)));
	B=floor(sqrt(n));
	fo(i,1,n)
	scanf("%d",&w[i]);
	fo(i,1,n-1)
	scanf("%d%d%d",&b[i].x,&b[i].y,&b[i].s);

	sort(b+1,b+(n-1)+1,cmp);

	fo(i,1,n+n-1)
	Fa[i]=i;

	fo(i,1,n)
	sum[i]=w[i];

	fo(i,1,n-1)
	{
		sum[n+i]=sum[gf(b[i].x)]+sum[gf(b[i].y)];

		fa[Fa[b[i].x]][0]=n+i;
		fa[Fa[b[i].y]][0]=n+i;
		son[n+i][0]=Fa[b[i].x];
		son[n+i][1]=Fa[b[i].y];

		Fa[Fa[b[i].x]]=n+i;
		Fa[Fa[b[i].y]]=n+i;

		v[n+i]=b[i].s;
	}
}

void build() //xushu
{
	int i,j,k,l;

	sort(A+L,A+R+1,Cmp);

	l=1;
	p[1]=N,bz[N]=1;

	fo(i,L,R)
	if (!l || p[l]!=A[i].x)
	{
		if (!l)
		p[++l]=A[i].x;
		else
		{
			k=lca(p[l],A[i].x);

			if (k==p[l])
			p[++l]=A[i].x,bz[p[l]]=1;
			else
			{
				while (l && !inc(p[l],k))
				{
					fa2[p[l]]=p[l-1];
					--l;
				}

				if (p[l]!=k)
				{
					fa2[p[l+1]]=k;
					p[++l]=k,bz[k]=1;
				}
			}

			p[++l]=A[i].x,bz[A[i].x]=1;
		}
	}
	fd(i,l,1)
	fa2[p[i]]=p[i-1];

	sort(A+L,A+R+1,Cmp2);

	tot=0;
	fo(i,1,N)
	if (bz[i])
	C[++tot]=i;
}

void dfs2() //others
{
	int i,T,t2;

	t2=1;
	d2[1][0]=N;
	d2[1][1]=0;
	while (t2)
	{
		T=t2;

		if (!d2[t2][1])
		Bz[d2[t2][0]]=bz[d2[t2][0]];

		if (d2[t2][1]<=1)
		{
			if (son[d2[t2][0]][d2[t2][1]])
			{
				++t2;
				d2[t2][0]=son[d2[T][0]][d2[T][1]];
				d2[t2][1]=0;
			}

			++d2[T][1];
		}
		else
		{
			if (!Bz[d2[t2][0]])
			Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);

			if (t2>1)
			Bz[d2[t2-1][0]]|=Bz[d2[t2][0]];
			--t2;
		}
	}
}

long long find(int t,int x)
{
	int i;
	long long ans=0;

	fo(i,l2[t],r2[t])
	ans=max(ans,d[i][0]*x+d[i][1]);

	if (l2[t]>r2[t]) return 0;
	if (l2[t]==r2[t]) return d[l2[t]][0]*x+d[l2[t]][1];

	int l=l2[t],r=r2[t]-1,mid;

	while (l<r)
	{
		mid=(l+r)/2;

		if (dx[mid]<=x)
		l=mid+1;
		else
		r=mid;
	}
	if (dx[l]<=x)
	++l;

	return d[l][0]*x+d[l][1];
}

void Init() //zhixian
{
	int I,i,j,k,l=0;
	long long K,B;

	fo(I,1,tot)
	{
		i=C[I];

		l2[i]=l+1;

		T=0;
		if (i>n)
		{
			T=1;
			c[1]=i;

			j=fa[i][0];
			while (j && !bz[j])
			{
				c[++T]=j;
				j=fa[j][0];
			}
		}
		else
		{
			j=fa[i][0];
			while (j && !bz[j])
			{
				c[++T]=j;
				j=fa[j][0];
			}
		}

		fd(j,T,1)
		{
			if (l2[i]>l)
			{
				++l;
				d[l][0]=v[c[j]];
				d[l][1]=sum[c[j]]*v[c[j]];
			}
			else
			{
				K=v[c[j]];
				B=sum[c[j]]*v[c[j]];

				while (l2[i]<l && dx[l-1]*K+B>=dx[l-1]*d[l][0]+d[l][1])
				--l;

				if (d[l][0]!=K)
				{
					++l;
					d[l][0]=K;
					d[l][1]=B;
					dx[l-1]=(double)(d[l][1]-d[l-1][1])/(d[l-1][0]-d[l][0]);
				}
			}
		}
		r2[i]=l;

		ANS[i]=find(i,0);
	}
}

void work(int t)
{
	while (t)
	{
		X[t]+=S;
		ANS[t]=find(t,X[t]);

		t=fa2[t];
	}
}

void find()
{
	int i;

	fo(i,1,tot)
	ans[A[I].id]=max(ans[A[I].id],ANS[C[i]]);
}

void Build()
{
	int i,T,t2;

	t2=1;
	d2[1][0]=N;
	d2[1][1]=0;
	while (t2)
	{
		T=t2;

		if (!d2[t2][1])
		sum[d2[t2][0]]=w[d2[t2][0]];

		if (d2[t2][1]<=1)
		{
			if (son[d2[t2][0]][d2[t2][1]])
			{
				++t2;
				d2[t2][0]=son[d2[T][0]][d2[T][1]];
				d2[t2][1]=0;
			}

			++d2[T][1];
		}
		else
		{
			if (!Bz[d2[t2][0]])
			Ans=max(Ans,sum[d2[t2][0]]*v[d2[t2][0]]);

			if (t2>1)
			sum[d2[t2-1][0]]+=sum[d2[t2][0]];
			--t2;
		}
	}
}

int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);

	init();

	N=n+n-1;
	j=0;
	dfs();

	fo(i,1,Q)
	scanf("%d%d",&A[i].x,&A[i].s),A[i].id=i;

	for (L=1; L<=Q; L+=B)
	{
		Ans=0;
		tot=0;
		T=0;

		R=min(L+B-1,Q);
		build();
		dfs2();
		Init();

		fo(I,L,R)
		{
			ans[A[I].id]=Ans;
			S=A[I].s-w[A[I].x];

			work(A[I].x);
			find();

			w[A[I].x]=A[I].s;
		}

		Build();

		fo(i,1,tot)
		bz[C[i]]=0,X[C[i]]=0;
	}

	fo(i,1,Q)
	printf("%lld\n",ans[i]);

	fclose(stdin);
	fclose(stdout);

	return 0;
}