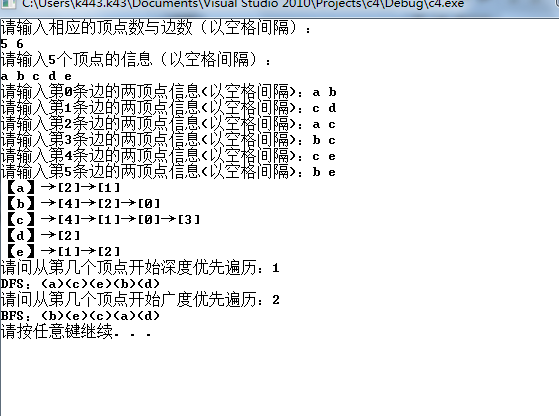
c++ 由无向图构造邻接表，实现深度优先遍历、广度优先遍历。

/*
首先，根据用户输入的顶点总数和边数，构造无向图，然后以用户输入的顶点
为起始点，进行深度优先、广度优先搜索遍历，并输出遍历的结果。
*/
#include <stdlib.h>
#include <iostream>
#define MVNum 100         //最大的顶点数
using namespace std;

/*——————图的邻接表存储表示——————*/
//边的结点表-在顶点表后面
typedef struct ArcNode
{
    int adjvex;                 //邻接点域-该边所指向顶点的位置下标
    struct ArcNode* nextarc; //链域-邻接的下一顶点位置
    //otherInfo info;        //用来纪录权值
}ArcNode;
//单链表表头-结构体（类似于头结点）
typedef struct VNode
{
    char data;                //顶点的信息值
    ArcNode* firstarc;        //指向第一条依附该顶点的下一结点-指向类型为边ArcNode
}VNode, AdjList[MVNum];        //AdjList邻接表类型
//图ALGraph
typedef struct
{
    AdjList vertices;        //定义一个邻接表类型，vertices最多有MVNum个
    int vexnum;                //顶点数
    int arcnum;                //边数
}ALGraph;
//链队列结构体
typedef struct QNode
{
    int data;
    struct QNode* next;
}QNode,*QueuePtr;
//链队头指针结构体
typedef struct
{
    QueuePtr front;  //队头
    QueuePtr rear;      //队尾
}LinkQueue;
//寻找v1，v2的下标
int LocateVex(ALGraph& G, char NodeInfo)
{
    int flag = ;
    //匹配NodeInfo
    for (int i = ; i < G.vexnum; i++)
    {
        if (G.vertices[i].data == NodeInfo)
        {
            flag = i;
            return i;
            break;
        }
    }
    if (flag)
        return flag;
    else
        exit(errno);
}
//邻接表生成无边图
void CreateUDG(ALGraph& G)
{
    //输入数据
    cout << "请输入相应的顶点数与边数（以空格间隔）：" << endl;
    cin >> G.vexnum >> G.arcnum;

    //初始化顶点信息
    cout << "请输入" << G.vexnum << "个顶点的信息（以空格间隔）：" << endl;
    for (int i = ; i < G.vexnum; i++)
    {
        cin >> G.vertices[i].data;
        G.vertices[i].firstarc = NULL;    //各顶点结点的指针域置空
    }

    //初始化边的连接信息
    for (int i = ; i < G.arcnum; i++)
    {
        char v1, v2;                        //v1,v2为一条边连接的两个顶点
        cout << "请输入第" << i << "条边的两顶点信息(以空格间隔)：";
        cin >> v1 >> v2;

        //求v1，v2在vertices的下标
        int idx_v1 = LocateVex(G, v1);
        int idx_v2 = LocateVex(G, v2);

        //调用边的结点表,生成以v1为头结点的单链表构成的邻接表
        ArcNode* p1 = new ArcNode;            //生成第一个边连接的结点（后面的那一个）
        p1->adjvex = idx_v2;                //存入结点的下标
        //关联头结点，用头插法，插入结点
        p1->nextarc = G.vertices[idx_v1].firstarc;
        G.vertices[idx_v1].firstarc = p1;

        //调用边的结点表,生成以v2为头结点的单链表构成的邻接表
        ArcNode* p2 = new ArcNode;            //生成第一个边连接的结点（后面的那一个）
        p2->adjvex = idx_v1;                //存入结点的下标
        //关联头结点，用头插法，插入结点
        p2->nextarc = G.vertices[idx_v2].firstarc;
        G.vertices[idx_v2].firstarc = p2;
    }
}
//邻接表的遍历
void TraverseAdjList(ALGraph& G)
{
    for (int i = ; i < G.vexnum; i++)
    {
        cout << "【" << G.vertices[i].data << "】→";
        //临时头指针用于遍历
        ArcNode* temp = G.vertices[i].firstarc;
        //当temp不为空，输出链表

        while (temp)
        {
            //输出顶点序号
            cout<<"["<<temp->adjvex<<"]";
            temp=temp->nextarc;
            if (temp)
                cout << "→";
        }
        putchar();
    }
}
//深度优先遍历
int visisted_D[MVNum] = {  };    //辅助数组
void DFS_AL(ALGraph& G, int v)
{
    //从v顶点开始访问
    cout <<"("<< G.vertices[v].data <<")";
    //访问过后置1
    visisted_D[v] = ;
    //临时结点用于遍历，指向头结点后一结点
    ArcNode *temp = G.vertices[v].firstarc;

    //循环遍历
    while (temp)
    {
        int w = temp->adjvex;
        //如果辅助数组visisted[w] == 0递归调用DFS_AL
        if (visisted_D[w] == )
        {
            DFS_AL(G, w);
        }
        //temp指向下一结点
        temp = temp->nextarc;
    }
}
//广度优先遍历
int visisted_B[MVNum] = {  };    //辅助数组
//队列初始化
void InitQuenue(LinkQueue& Q)
{
    Q.rear = new QNode;
    Q.front = Q.rear;
    Q.front->next = NULL;
}
//入队-尾插法
void EnQuenue(LinkQueue& Q,int v)
{
    QNode* cur = new QNode;
    cur->data = v;
    cur->next = NULL;
    Q.rear->next = cur;
    Q.rear = cur;
}
//出队-返回队头int u
void DeQuenue(LinkQueue& Q, int &u)
{
    QNode* temp = Q.front->next;
    Q.front->next = temp->next;
    //队头u更新
    u = temp->data;
    //如果最后一个被删，队尾指向队头
    if (Q.rear == temp)
    {
        Q.rear = Q.front;
    }
    delete temp;
}
//返回u的第一个邻结点
int FirstAdjvex(ALGraph& G, int u)
{
    int w = G.vertices[u].firstarc->adjvex;
    return w;
}
//返回u的下一个邻结点
int NextAdjVex(ALGraph& G, int u, int w)
{
    //临时结点temp指向头结点的第一个邻结点，w此时为第一结点序号
    ArcNode *temp = G.vertices[u].firstarc;
    while (temp->adjvex != w)
    {
        temp = temp->nextarc;
    }
    //若w结点的下一结点不为空，返回结点序号w的下一结点序号
    if (temp->nextarc)
        return temp->nextarc->adjvex;
    //否则返回-1，使其退出循环
    else
        return -;
    delete temp;
}
void BFS_AL(ALGraph& G, int v)
{
    //从v顶点开始访问
    cout << "(" << G.vertices[v].data << ")";
    //访问过后置1
    visisted_B[v] = ;
    //创建队列
    LinkQueue Q;
    InitQuenue(Q);
    EnQuenue(Q,v);
    int u = v;        //用于找邻接点
    //队列非空出队
    while (Q.rear != Q.front)
    {
        //出队，并把队头置为u
        DeQuenue(Q, u);
        for (int w = FirstAdjvex(G, u); w >= ; w = NextAdjVex(G, u, w))
        {
            //若结点序号w未访问则进行访问
            if (!visisted_B[w])
            {
                cout << "(" << G.vertices[w].data << ")";        //输出数据
                visisted_B[w] = ;                //打上访问标记
                EnQuenue(Q, w);                    //将结点w入队
            }
        }//进行下一次w的邻结点查找
    }
}
void main()
{
    ALGraph G;
    //邻接表生成无边图

    CreateUDG(G);
    //遍历邻接表
    TraverseAdjList(G);
    //深度优先遍历
    cout << "请问从第几个顶点开始深度优先遍历：";
    int v;
    cin >> v;
    cout << "DFS：";
    DFS_AL(G, v-);
    putchar();
    //广度优先遍历
    cout << "请问从第几个顶点开始广度优先遍历：";
    cin >> v;
    cout << "BFS：";
    BFS_AL(G, v - );
    putchar();
    system("pause");
}

//深度优先遍历由递归实现。也可用栈来实现（与BFS队列操作类似）。

//广度优先遍历由队列实现。需要先让开始进行遍历的顶点入队，再进行出队，但是出队需保存出队的结点序号值作为表头，用于遍历该层，并同时将辅助数组visisted_B[v]置为1，以表示已经访问，然后根据邻接表结构进行类似于树的层次遍历操作，每个结点访问过后都要将visisted_B[v]置为1，当其中一层遍历完过后，先进的第一个结点出队，并更新出队值，同时开始遍历以该结点序号为头结点的单链表，直到每层遍历完后结束。
//在广度优先遍历过程中，进行出队操作时，一开始用形参int u来进行接收，导致队头值u（表头）无法更新，造成只能遍历初始顶点的那一条单链表，后改为形参 int &u解决队头值更新问题。