matplotlib实现数据可视化

一篇matplotlib库的学习博文。matplotlib对于数据可视化非常重要，它完全封装了MatLab的所有API，在python的环境下和Python的语法一起使用更是相得益彰。

一、库的安装和环境的配置

windows下：py -3 -m pip install matplotlib

linux下：python3 -m pip install matplotlib

建议配合Jupyter使用。在jupyter notebook中，使用%matplotlib inline，即可进入交互页面（类似下图）

二、设置中文环境

首先引入包：

import numpy as np #之后需要用到
import matplotlib as mpl #设置环境变量
import matplotlib.pyplot as plt #绘图专用
from mpl_toolkits.mplot3d import Axes3D #绘制3D图

为了让图片兼容中文的说明、名字等，这里需要：

mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus']=False

三、一窥全貌

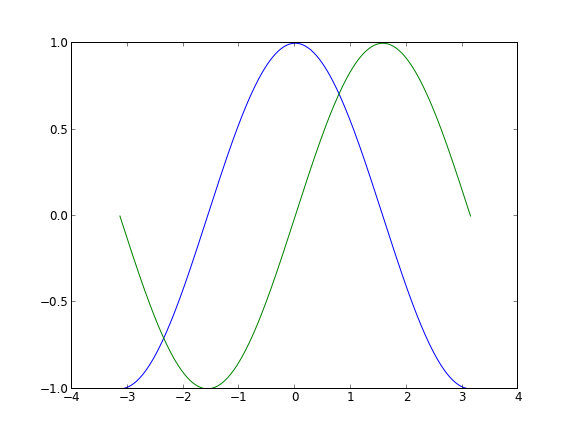
首先，我们画一张正弦和余弦图。

plt.figure('sin/cos', dpi=70)
# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
plt.subplot(1,1,1)
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
# 绘制余弦曲线，使用蓝色的、连续的、宽度为 1 （像素）的线条
plt.plot(X, C, color="blue", linewidth=1.0, linestyle="-")
# 绘制正弦曲线，使用绿色的、连续的、宽度为 1 （像素）的线条
plt.plot(X, S, color="green", linewidth=1.0, linestyle="-")
# 设置横轴的上下限
plt.xlim(-4.0,4.0)
# 设置横轴记号
plt.xticks(np.linspace(-4,4,9,endpoint=True))
# 设置纵轴的上下限
plt.ylim(-1.0,1.0)
# 设置纵轴记号
plt.yticks(np.linspace(-1,1,5,endpoint=True))
# 以分辨率 72 来保存图片
# savefig("exercice_2.png",dpi=72)
# 在屏幕上显示
plt.show()

1. plt.figure(name,dpi):name是图片的名字，dpi是分辨率
2. plt.plot(x,y,color,linewidth,linestyle,label)：用来绘制点线图。color是线条颜色，linewidth是宽度，linestyle可以设置成--，就变成了虚线。
   
   label参数和图例有关
3. plt.xlim(min,max)/plt.ylim(min,max)：设置x/y轴的范围。
4. plt.xtricks(列表)/plt.ytricks(列表)：设置x轴/y轴的上显示的值。
   
   如果想要设置记号标签（我们可以把 3.1423.142 当做是 ππ，但毕竟不够精确。当我们设置记号的时候，我们可以同时设置记号的标签。注意这里使用了 LaTeX）。可以传入两个对应的列表。
5. plt.legend(loc=随机默认)：添加图例，图例来自于plt.plot()参数里的label，如果想让label按照公式显示，需要在字符串前后加$。即：label='$sin(x)$'
   
   loc参数定义图标位置，可以是upper left/right类似的方向。
6. plt.xlabel(labelname)/ylabel(labelname)：添加x/y轴的名字并且显示出来。
7. plt.scatter(xlist,ylist):根据需要标注图中的特殊点。
8. plt.title()：给图一个名字
9. 移动坐标轴：（之前的图片还是不好看）实际上每幅图有四条脊柱（上下左右），为了将脊柱放在图的中间，我们必须将其中的两条（上和右）设置为无色，然后调整剩下的两条到合适的位置——数据空间的 0 点。

ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('red')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

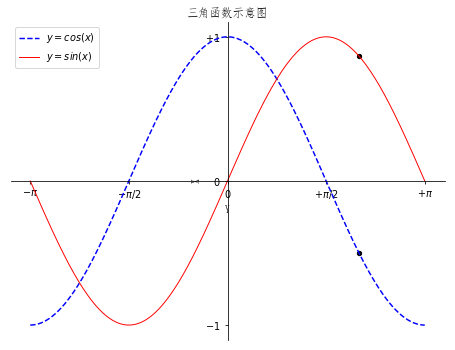
改进后的代码如下：

plt.figure(figsize=(8,6), dpi=70)

# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
plt.subplot(1,1,1)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plt.plot(X, C, color="blue", linewidth=1.5, linestyle="--",label="$y=cos(x)$")
plt.plot(X, S, color="red", linewidth=1.0, linestyle="-",label='$y=sin(x)$')

plt.xlabel('Y')
plt.ylabel('X')

plt.xlim(X.min()*1.1,X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],\
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, 0, +1],\
       [r'$-1$', r'$0$', r'$+1$'])

ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
# 以分辨率 72 来保存图片
# savefig("exercice_2.png",dpi=72)

t = 2*np.pi/3
plt.scatter([t,],[np.cos(t),], 20, color ='black')
plt.scatter([t,],[np.sin(t),], 20, color ='black')

plt.legend(loc="upper left")
plt.title('三角函数示意图')
# 在屏幕上显示
plt.show()

现在来看一下处理过后的图的样子：

---

欢迎进一步交流本博文相关内容：

博客园地址 : http://www.cnblogs.com/AsuraDong/

CSDN地址 : http://blog.csdn.net/asuradong

也可以致信进行交流 : xiaochiyijiu@163.com

欢迎关注个人微博：http://weibo.com/AsuraDong

欢迎转载 , 但请指明出处  :  )

---

四、精益求精

plt.figure('sin/cos', dpi=70)

# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
#plt.subplot(112)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plt.plot(X, C, color="blue", linewidth=1.5, linestyle="--",label="$y=cos(x)$")
plt.plot(X, S, color="red", linewidth=1.0, linestyle="-",label='$y=sin(x)$')

plt.xlabel('Y')
plt.ylabel('X')

plt.xlim(X.min()*1.1,X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],\
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, 0, +1],\
       [r'$-1$', r'$0$', r'$+1$'])

ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
# 以分辨率 72 来保存图片
# savefig("exercice_2.png",dpi=72)

t = 2*np.pi/3
plt.scatter([t,],[np.cos(t),], 20, color ='black')
plt.scatter([t,],[np.sin(t),], 20, color ='black')

plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',\
         xy=(t, np.sin(t)), xycoords='data',\
         xytext=(+10, +30), textcoords='offset points', fontsize=16,\
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',\
         xy=(t, np.cos(t)), xycoords='data',\
         xytext=(-90, -50), textcoords='offset points', fontsize=16,\
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plt.plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--")
plt.plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")

plt.legend(loc="upper left")
plt.title('三角函数示意图')
# 在屏幕上显示
plt.show()

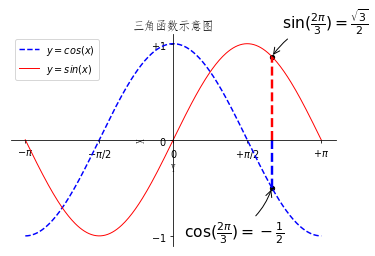
我们添加了标注点，并且向x轴做了垂线，使其更清晰。

五、图的存储

这么漂亮的图，还是通过plt.savefig(照片名字+后缀名)保存到本地吧。

六、子图

plt.subplot(x,y,n):将图片分成x*y块，这个图是第n个。（看示例）

示例一：

x = np.arange(0, 5, 0.1)
y = np.arange(0, 5, 0.1)  

#plt.figure(1)
plt.subplot(221)
plt.plot(x, y, 'go')

plt.subplot(222)
plt.plot(x, y, 'r--')  

plt.subplot(212)
plt.plot(x, y,)  

plt.show()

示例二：

x = np.arange(0, 5, 0.1)
y = np.arange(0, 5, 0.1)  

#plt.figure(1)
plt.subplot(221)
plt.plot(x, y, 'go')

plt.subplot(222)
plt.plot(x, y, 'r--')  

plt.subplot(224)
plt.plot(x, y,)  

plt.show()

致谢

译文作者

原文大神