机器学习：保序回归(IsotonicRegression)：一种可以使资源利用率最大化的算法

1.数学定义

保序回归是回归算法的一种,基本思想是：给定一个有限的实数集合,训练一个模型来最小化下列方程：

并且满足下列约束条件：

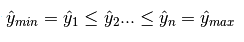
2.算法过程说明

从该序列的首元素往后观察，一旦出现乱序现象停止该轮观察，从该乱序元素开始逐个吸收元素组成一个序列，直到该序列所有元素的平均值小于或等于下一个待吸收的元素。

举例：

原始序列：<9, 10, 14>

结果序列：<9, 10, 14>

分析：从9往后观察，到最后的元素14都未发现乱序情况，不用处理。

原始序列：<9, 14, 10>

结果序列：<9, 12, 12>

分析：从9往后观察，观察到14时发生乱序（14>10），停止该轮观察转入吸收元素处理，吸收元素10后子序列为<14, 10>，取该序列所有元素的平均值得12，故用序列<12, 12>替代<14, 10>。吸收10后已经到了最后的元素，处理操作完成。

原始序列：<14, 9, 10, 15>

结果序列：<11, 11, 11, 15>

分析：从14往后观察，观察到9时发生乱序（14>9），停止该轮观察转入吸收元素处理，吸收元素9后子序列为<14,9>。求该序列所有元素的平均值得12.5，由于12.5大于下个待吸收的元素10，所以再吸收10，得序列<14, 9, 10>。求该序列所有元素的平均值得11，由于11小于下个待吸收的元素15，所以停止吸收操作，用序列<11, 11, 11>替代<14, 9, 10>。

3.举例说明下面实验的原理

以某种药物的使用量为例子：

假设药物使用量为数组X=0,1,2,3,4….99，病人对药物的反应量为Y=y₁,y₂,y₃…..y₉₉ ，而由于个体的原因，Y不是一个单调函数(即：存在波动)，如果我们按照药物反应排序，对应的X就会成为乱序，失去了研究的意义。而我们的研究的目的是为了观察随着药物使用量的递增，病人的平均反应状况。在这种情况下，使用保序回归，即不改变X的排列顺序，又求的Y的平均值状况。如下图所示：

从图中可以看出，最长的绿线x的取值约是30到60，在这个区间内，Y的平均值一样，那么从经济及病人抗药性等因素考虑，使用药量为30个单位是最理想的。

当前IT行业虚拟化比较流行，使用这种方式，找到合适的判断参数，就可以使用此算法使资源得到最大程度的合理利用。

4.实验代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state

n = 100
##产生一个0-99的列表
x = np.arange(n)
##实例化一个np.random.RandomState的实例，作用是每次取的随机值相同
rs = check_random_state(0)
##randint(-50, 50)：产生-50到50之间的整数
##np.log  求以e为低的对数
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log(1 + np.arange(n))

##设置保序回归函数
ir = IsotonicRegression()
##训练数据
y_ = ir.fit_transform(x, y)

##绘图
segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
##plt.gca().add_collection(lc),这两步就是画点与平均直线的连线
lc = LineCollection(segments)

fig = plt.figure()
plt.plot(x, y, 'r.', markersize=12)
plt.plot(x, y_, 'g.-', markersize=12)
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit'), loc='lower right')
plt.title('Isotonic regression')
plt.show()