神经网络NN笔记

参考：http://www.cnblogs.com/subconscious/p/5058741.html

俗话说，好记性不如烂笔头~~~~

边学边记，方便以后查找~~~~~

一、介绍一下经典的神经网络

这个是人脑的神经网络，是不是很复杂啊~~~~~~科普成人的大脑里有1000亿的神经元（但怎么感觉大脑不够用啊~~~~可怕）

我来盗一波图~~~哈哈

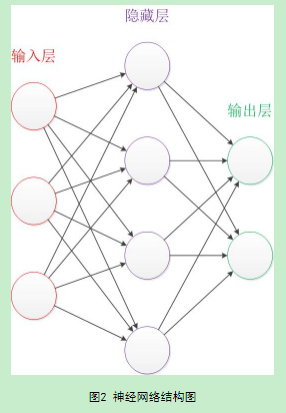
上图2是经典的神经网络图，其中包括输入层3个，隐藏层4个，输出层2个。在设计一个神经网络的时候，输入层和输出层的节点数往往是固定不变的，中间的隐藏层则是自由指定的。这个结构图中的拓扑与箭头代表预测过程时数据的流向，但是这个和训练时还是有一定的区别的~~~~

重要的来了。。图2的一个圆圈代表一个神经元，连接线代表神经元之间的连接，每个连接线对应一个不同的权重，权重的值叫做权值，需要通过训练获得的。

 二、神经元

盗图的感觉真棒啊~~~~~

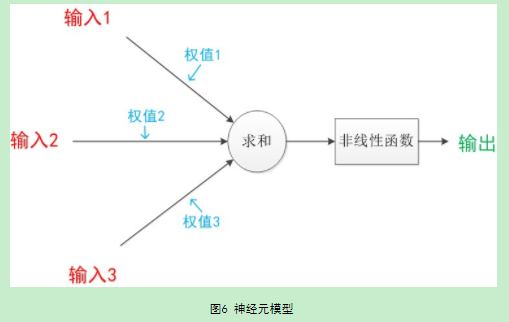
一个神经元的模型，包含输入，输出与计算功能的模型，上图就是3个输入，2个计算功能，1个输出，这些线每个都有一个权值。

（我有一个大胆的想法，可不可以把神经网络缩小化，变成一个神经元~~~两者真的很像）

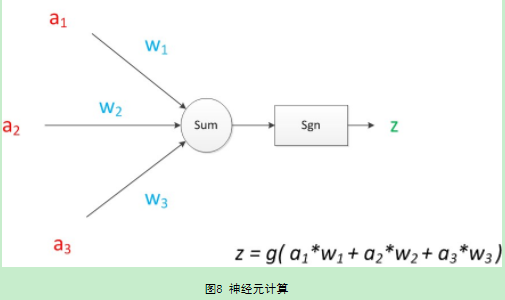
由上图知，z是在输入和权值的线性加权和套了一个函数g的值。

神经元模型的使用时，可以这样理解:假设一个数据data，称之为样本。样本有4个属性，其中三个属性为已知a1,a₂,a₃,，一个属性为未知,z。我们需要做的是通过三个已知属性预测未知属性，z

z可以通过公式计算出来。

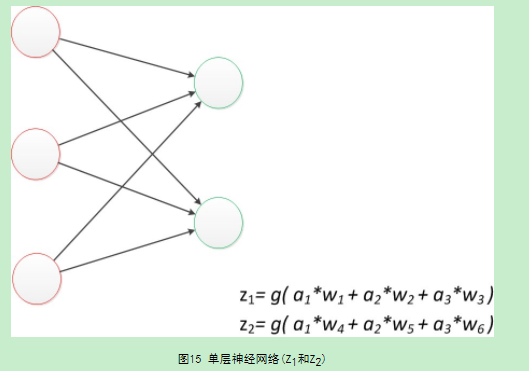
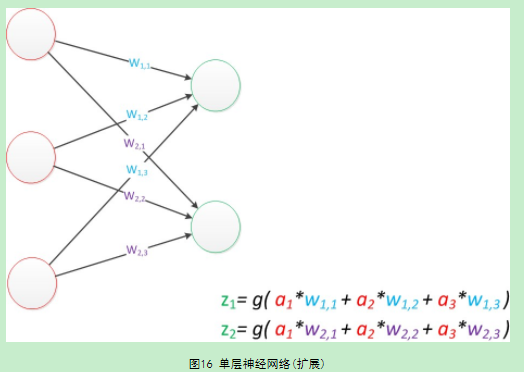
w权值的之间关系用矩阵表示

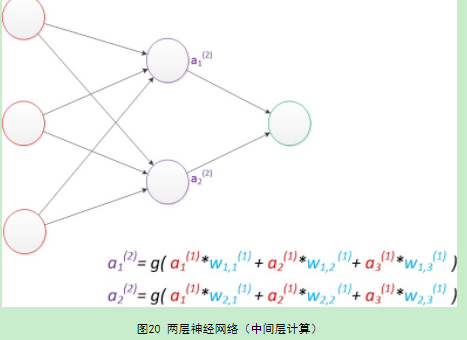
如图，两层的神经网络结构，

三、RNN / CNN/DNN

1.DNN神经网络有深度~~~~

2.CNN卷积神经网络

有时候参数数量的膨胀，容易过拟合，极易陷入局部最优。需要用‘卷积核’作为中介。同一个卷积核在所有图像内是共享的，图像通过卷积操作后仍然保留原先的位置关系。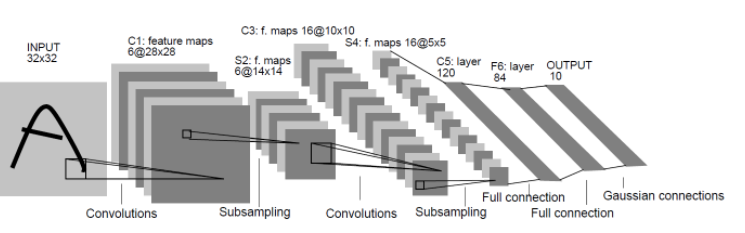

3.RNN循环神经网络

因为全连接的DNN有一个问题---------无法对时间序列上的变化进行建模。

然而，样本出现时间顺序对于自然语言处理、语音识别等应用非常重要。

对了适应这种需求，RNN循环神经网络。

在RNN中，神经元的输出可以在下一个时间戳直接作用到自身（第i层神经元在m时刻的输入，除了（i-1）层神经元在该时刻的输出外，还包括其自身在（m-1）时刻的输出）

RNN可以看成一个在时间上传递的神经网络，深度是时间的长度~~~

然而梯度消失现象还是要出现，且发生在时间轴上。对于t时刻来说，它产生的梯度在时间轴上向历史传播层之后就消失了，所以无法影响太遥远的过去。