POJ 3154 Graveyard【多解，数论，贪心】

Graveyard

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1707		Accepted: 860		Special Judge

Description

Programming contests became so popular in the year 2397 that the governor of New Earck — the largest human-inhabited planet of the galaxy — opened a special Alley of Contestant Memories (ACM) at the local graveyard. The ACM encircles a green park, and holds the holographic statues of famous contestants placed equidistantly along the park perimeter. The alley has to be renewed from time to time when a new group of memorials arrives.

When new memorials are added, the exact place for each can be selected arbitrarily along the ACM, but the equidistant disposition must be maintained by moving some of the old statues along the alley.

Surprisingly, humans are still quite superstitious in 24th century: the graveyard keepers believe the holograms are holding dead people souls, and thus always try to renew the ACM with minimal possible movements of existing statues (besides, the holographic equipment is very heavy). Statues are moved along the park perimeter. Your work is to find a renewal plan which minimizes the sum of travel distances of all statues. Installation of a new hologram adds no distance penalty, so choose the places for newcomers wisely!

Input

Input file contains two integer numbers: n — the number of holographic statues initially located at the ACM, and m — the number of statues to be added (2 ≤ n ≤ 1000, 1 ≤ m ≤ 1000). The length of the alley along the park perimeter is exactly 10 000 feet.

Output

Write a single real number to the output file — the minimal sum of travel distances of all statues (in feet). The answer must be precise to at least 4 digits after decimal point.

Sample Input

sample input #1
2 1

sample input #2
2 3

sample input #3
3 1

sample input #4
10 10

Sample Output

sample output #1
1666.6667

sample output #2
1000.0

sample output #3
1666.6667

sample output #4
0.0

Hint

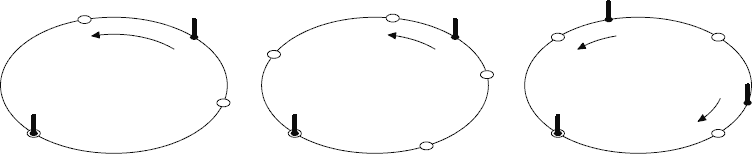
Pictures show the first three examples. Marked circles denote original statues, empty circles denote new equidistant places, arrows denote movement plans for existing statues.

Source

Northeastern Europe 2006

题目链接：http://poj.org/problem?id=3154

题意：一个圆上原先均匀分布着n个点（可移动），现要加入新的m个点，使（n+m）个点仍然均匀分布在圆上，m个点可任意加在任意位置，求重新均匀分布时，原来n个点的移动距离的和的最小值。

这是lrj大白书上的一道题目（P7）。

数论解法：

证明思路，证明这个算法需要证明两个结论：

结论一：无论新的方案和旧的方案的相对位置是什么样的，对于原先的n个点来说，最好的策略就是往最近的新点位置上走。

这个结论唯一一个需要想一下的地方是，两个旧点会不会站到一个坑里去。可以证明这是不会的，设旧的方案两个点之间距离为L，新的方案两个点之间距离为X,若两个旧点A，B跑到了同一个新点O上,就说明，|AO| < x/2 && |AB| < x/2 ，则L = |AB| <= |AO| + |BO| < 2*(X/2)  = X ,但事实上，L  > X。反正就是不会碰在一起。

结论二：在结论一的前提下，有至少一个点重合的方案是最佳方案。

首先，一开始是n个点，后来是n+m个点，就是说一开始间隔是1/n,后来是1/(n+m)。为了但是用分数看实在不方便，我们取1/（n*(n+m)）为基本单位，这样，旧的间隔是n+m，后来的间隔是n。在这里请假设n与n+m互质，如果不是互质，我们就进行约分，原因后来会知道。

然后，我们先假设有新的方案和旧的方案有一个点是重合的，其中红色的线段和点是旧的方案，蓝色的是新的方案；

然后我们沿着这个重合的点，将圆环剪开，注意首尾相同，颜色没有变哦。

你有看出什么东西吗？好吧，如果没有，那么请你看下一步，将AB‘，B’D , DC'，C'A线段（即所有的蓝色点间隔形成的线段）重合。

好吧，让我们从代数的角度重新审视一下上面这个东西。设k = n+m，已经保证了k和n是互质的。看下面这段代码。

for（int i=;i<n;i++）
    a[i] = i*k%n;
sort（a,a+n）;

在这之后，如果你输入数组a的值，你会得到0,1,2,3....n-1，这样的序列。这是由两个数互质的性质决定的，具体证明可以采用反证法。

然后说了那么多，这个和我们的结论有什么关系呢？

既然所有的节点都到了一段区间，我们就不用管它到底是一个圆还是一条线段，从上面那个图上可以直接看出，B应该往左靠，C应该往右靠。

如果在这种情况下，我们选择转动A点，没转动x，A到最近点的距离增大x，B到最近点的距离增大x,C到最近点的距离减少x，B，C的影响抵消，所以总距离增大，这个增大的趋势一直到A,B,C三个点移动到了四等分该线段的时候，

,

然后A的最短距离增大，B,C的最短距离减少，总体距离减少。但是最终再次形成重合的时候，又是一样的。所以先增后尖，最小值在两端。

综合结论1,2该问题圆满解决。也因此获得了上面那个算法，一开始就将所有的关系投影到一个线段上。那个累加ans过程就来自以上分析。

值得一提的是，如果不进行约分的话，在很多情况下，答案也是对的，得益于映射到线段时良好的对称性。但是n和m存在倍数关系就不行了。

 #include <stdio.h>
 #define min(a,b) (a)>(b)?(b):(a)
 int gcd(int a,int b)
 {
     return b==?a:gcd(b,a%b);
 }
 int main()
 {
     int n,m;
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         int temp=gcd(n,m);
         n/=temp;
         m/=temp;
         int ans=;
         for(int i=;i<n;i++)
             ans+=min(i,n-i);
         printf("%.4lf\n",(double)ans/(n*(n+m))*);
     }
     return ;
 }

lrj解法(直接贪心，然后求最小距离(按比例缩小))：

 #include <stdio.h>
 #include <math.h>
 int main()
 {
     int n,m;
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         double ans=0.0;
         for(int i=;i<n;i++)
         {
             double pos=(double)i/n*(n+m);
             ans+=fabs(pos-floor(pos+0.5))/(n+m);
         }
         printf("%.4lf\n",ans*);
     }
     return ;
 }