p211有界自共轭算子T是实数集合的子集


对条件 取非
是 ∉谱集合的实数 才对
现在是 入 属于正则点集
他 然后 又说T 的谱是实数
这不矛盾吗
这里根据 
必要性 推出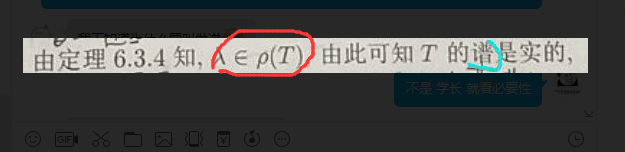
蓝色和红色矛盾
矛盾就是 这是谱点
然后 T优势自共轭的
所以 (Tx.x)=(入x,x)=入(x,x) =(x,Tx)=(Tx,x)的共轭 等于入(x,x)的共轭
所以入 等于 入共轭 所以 入是实数
p211有界自共轭算子T是实数集合的子集的更多相关文章
- python 实现求一个集合的子集
概要 今天偶然看到有个关于数学中集合的问题,就突发奇想的想用python实现下求一个集合的子集. 准备 我当然先要复习下,什么是集合,什么是子集? 比较粗犷的讲法,集合就是一堆确定的东西,细致一点的讲 ...
- [python语法]python中如何判断一个集合是另一个集合的子集?
问:python中如何判断一个集合是另一个集合的子集? 答:用issubset()方法 语法: A.issubset(B) 返回: True 如果A是B的子集. False 如果A不是B的子集. 样例 ...
- 59-python基础-python3-集合-集合常用方法-判断一个集合是否是另一个集合的子集-issubset()-issuperset()
判断一个集合是否是另一个集合的子集-issubset()-issuperset() 1-issubset() s1.issubset(s) 判断s1是否是s的子集 2-issuperset() 与is ...
- C#中判断一个集合是另外一个集合的子集
有这样的两个集合: string[] bigArr = new string[] { "a", "b", "c" };string[] sm ...
- UVA 11825 Hackers’ Crackdown(集合动态规划 子集枚举)
Hackers’ Crackdown Miracle Corporations has a number of system services running in a distributed com ...
- 78. Subsets(中等,集合的子集,经典问题 DFS)
Given a set of distinct integers, nums, return all possible subsets. Note: The solution set must not ...
- UVA11825 Hacker's Crackdown 二进制集合+关于子集的动态规划
题意:有N台服务器,全部服务器都直接运行着完全相同的N个任务.对于每台电脑,你都可以进行“一次”操作,使得某(自己选定)一种任务停止,且同时会使得其他和这台服务器直接相连的电脑上面相同的服务完全终止. ...
- 算法笔记-- 二进制集合枚举子集 && 求子集和 && 求父集和
枚举子集: 复杂度:O(2^k) )&s); 用sos dp求解子集和以及父集和 子集和: ; i <= k; i--) { ; mask < (<<k); mask+ ...
- 5-python的封装与结构 - set集合
目录 1 封装与解构 1.1 封装 1.2 解构 1.3 Python3的解构 2 set类型 2.1 set的定义 2.2 set的基本操作 2.2.1 增加元素 2.2.2 删除元素 2.2.3 ...
随机推荐
- c指针类型的作用
指针类型的作用 任何类型的指针占用的空间大小都是相同的(32位CPU是4字节:64位CPU是8字节) 既然任何类型的指针占用的空间大小都是相同的,为什么指针还需要类型呢?指针只是指向了一个内存地址,但 ...
- Cs231n课堂内容记录-Lecture 4-Part1 反向传播及神经网络
反向传播 课程内容记录:https://zhuanlan.zhihu.com/p/21407711?refer=intelligentunit 雅克比矩阵(Jacobian matrix) 参见ht ...
- SQLServer数据库增删改查
一.数据库定义 数据库(Database)是按照数据结构来组织.存储和管理数据的仓库.数据库的操作分为两种形式:一种是直接在数据库管理工具图形化界面进行操作:一种是使用数据库脚本进行操作,数据库脚本可 ...
- 爬楼梯的golang实现
假设你正在爬楼梯.需要 n 阶你才能到达楼顶. 每次你可以爬 1 或 2 个台阶.你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数. 输入: 输出: 解释: 有两种方法可以爬到楼顶. ...
- vue中父组件调用子组件函数
用法: 子组件上定义ref="refName", 父组件的方法中用 this.$refs.refName.method 去调用子组件方法 详解: 父组件里面调用子组件的函数,父组 ...
- (转)Spring Boot 2 (八):Spring Boot 集成 Memcached
http://www.ityouknow.com/springboot/2018/09/01/spring-boot-memcached.html Memcached 介绍 Memcached 是一个 ...
- react中使用Ajax请求(axios,Fetch)
React本身只关注于界面, 并不包含发送ajax请求的代码,前端应用需要通过ajax请求与后台进行交互(json数据),可以使用集成第三方ajax库(或自己封装) 常用的ajax请求库 jQuery ...
- centos7下安装docker(15.2跨主机网络-overlay)
为支持容器跨主机通信,Docker提供了overlay driver,使用户可以创建基于VxLAN的overlay网络.VxLAN可将二层数据封装到UDP进行传输,VxLAN提供与VLAN相同的以太网 ...
- redis加锁
1. redis加锁分类 redis能用的的加锁命令分表是INCR.SETNX.SET2. 第一种锁命令INCR 这种加锁的思路是, key 不存在,那么 key 的值会先被初始化为 0 ,然后再执行 ...
- mysql远程连接 Host * is not allowed to connect to this MySQL server
mysql -u root -p mysql>use mysql; mysql>update user set host =’%'where user =’root’; mysql> ...
