【UR #3】链式反应

http://uoj.ac/problem/50

%炮姐

好博客

树形结构

枚举根节点的儿子是哪两个

然后列出方程：

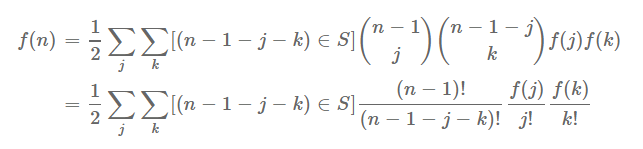
然后有EGF的影子！

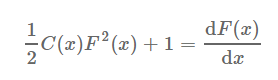
倍增？

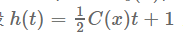
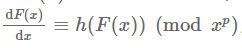
泰勒展开可以把未知数从函数里拿出来！并且变成1次项，

只要计算h(F0(x))以及h'(F0(x))

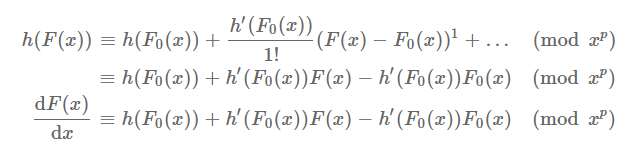
考虑把F(x)有关项移到左边

想办法把导数或者积分放到等号右边

乘上一个关键的v(x)

因为这个东西可以和F(x)的系数凑成v'(x)

然后函数相乘求导的逆运算凑回去

左边都是导数啦

直接积分，再除过去v(x)，

就可以直接倍增啦！！

多项式全家桶

il Poly sol(const Poly &C,int n){
    if(n==){
        Poly f0;f0.resize();f0[]=;f0[]=;
        return f0;
    }
    Poly f0=sol(C,(n+)>>);
    Poly tmp;tmp.resize(n);
    for(reg i=;i<n;++i){
        tmp[i]=C[i];
    }
    Poly lp=tmp*f0;
    lp.resize(n);
    Poly v=Exp(Inter(lp));
    v.resize(n);
    lp=lp*f0;
    lp.resize(n);
    tmp=Inv(v,v.size())*(lp*(mod-iv2)+);
    tmp.resize(n);
    tmp=v*Inter(tmp);
    tmp.resize(n);
    return tmp;
}

注意是生成函数，C开始是1/i!，最后得到的F要乘上i!