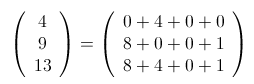hdu 1907 (尼姆博弈)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1907
Both of players are using optimal game strategy. John starts first always. You will be given information about M&Ms and your task is to determine a winner of such a beautiful game.
Constraints:
1 <= T <= 474,
1 <= N <= 47,
1 <= Ai <= 4747
1、问题模型:有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
2、解决思路:用(a,b,c)表示某种局势,显证(0,0,0)是第一种奇异局势,无论谁面对奇异局势,都必然失败。第二种奇异局势是(0,n,n),只要与对手拿走一样多的物品,最后都将导致(0,0,0)。
搞定这个问题需要把必败态的规律找出:(a,b,c)是必败态等价于a^b^c=0(^表示异或运算)。
证明:(1)任何p(a,b,c)=0的局面出发的任意局面(a,b,c’);一定有p(a,b,c’)不等于0。否则可以得到c=c’。
(2)任何p(a,b,c)不等于0的局面都可以走向 p(a,b,c)=0的局面
(3)对于 (4,9,13) 这个容易验证是奇异局势
其中有两个8,两个4,两个1,非零项成对出现,这就是尼姆和为 零的本质。别人要是拿掉13里的8或者1,那你就拿掉对应的9 中的那个8或者1;别人要是拿 掉13里的4,你就拿掉4里的4; 别人如果拿掉13里的3,就把10作分解,然后想办法满 足非零项成对即可。
3、推广一:如果我们面对的是一个非奇异局势(a,b,c),要如何变为奇异局势呢?假设 a < b< c,我们只要将 c 变为 a^b,即可,因为有如下的运算结果: a^b^(a^b)=(a^a)^(b^b)=0^0=0。要将c 变为a^b,只从 c中减去 c-(a^b)
4、推广二:当石子堆数为n堆时,则推广为当对每堆的数目进行亦或之后值为零是必败态。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<map>;
using namespace std;
int n,m,a[];
int main(){
int T;
cin>>T;
while(T--){
cin>>n;
int flag=;
for(int i=;i<=n;i++){
cin>>a[i];
if(a[i]!=)flag=;
}
if(!flag){
if(n%)puts("Brother");
else puts("John");
continue;
}
int ans=;
for(int i=;i<=n;i++)
ans^=a[i];
if(ans)puts("John");
else puts("Brother");
}
return ;
}
hdu 1907 (尼姆博弈)的更多相关文章
- hdu 1907 尼姆博弈
John Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)Total Submis ...
- hdu 1850(尼姆博弈)
Being a Good Boy in Spring Festival Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32 ...
- POJ 3480 & HDU 1907 John(尼姆博弈变形)
题目链接: PKU:http://poj.org/problem? id=3480 HDU:http://acm.hdu.edu.cn/showproblem.php? pid=1907 Descri ...
- hdu 1849 (尼姆博弈)
http://acm.hdu.edu.cn/showproblem.php? pid=1849 简单的尼姆博弈: 代码例如以下: #include <iostream> #include ...
- HDU.1850 being a good boy in spring festival (博弈论 尼姆博弈)
HDU.1850 Being a Good Boy in Spring Festival (博弈论 尼姆博弈) 题意分析 简单的nim 博弈 博弈论快速入门 代码总览 #include <bit ...
- hdu 1849(Rabbit and Grass) 尼姆博弈
Rabbit and Grass Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) ...
- HDU 4315 Climbing the Hill (阶梯博弈转尼姆博弈)
Climbing the Hill Time Limit: 1000MS Memory Limit: 32768KB 64bit IO Format: %I64d & %I64u Su ...
- HDU 2176 取(m堆)石子游戏 尼姆博弈
题目思路: 对于尼姆博弈我们知道:op=a[1]^a[2]--a[n],若op==0先手必败 一个简单的数学公式:若op=a^b 那么:op^b=a: 对于第i堆a[i],op^a[i]的值代表其余各 ...
- 题解报告:hdu 1850 Being a Good Boy in Spring Festival(尼姆博弈)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1850 Problem Description 一年在外 父母时刻牵挂春节回家 你能做几天好孩子吗寒假里 ...
随机推荐
- Jenkins+Docker自动化集成环境搭
关于Docker Docker 简介 Docker现在是Github社区最火的项目之一,Docker是个容器,或许你听过lxc,你可能知道Tomcat这个Web容器,容器是什么概念,意会就好.问个问题 ...
- java的编程习惯影响程序性能
在Java程序中,性能问题的大部分原因并不在于Java语言,而是在于程序本身. 养成良好的编程习惯非常重要,能够显著地提升程序性能. 尽量在合适的场合使用单例 使用单例可以减轻加载的负担,缩短加载的时 ...
- 编写自己的composer项目
编写自己的composer项目 composer的出现给php开发带来极大的便利, 配合phpunit的测试工具, 也可以更好的规范php开发. 尽管这些标准不是官方提供的, 但现在大部分的php ...
- Eclipse打开java文件繁体字
右键-->properties-->Resource-->Text file encoding, 改成utf-8 .
- 本地上传项目到github
https://www.cnblogs.com/rosej/p/6056467.html(copy)
- day 7-17 多表查询
一. 准备表 #部门表 create table dep( id int, name varchar(20) ); #员工表 create table emp( id int primary key ...
- JSON Support in PostgreSQL and Entity Framework
JSON 和JSONB的区别(What's difference between JSON and JSONB data type in PosgresSQL?) When should be use ...
- Python模拟wc命令(软件测试第二次作业)
Python实现字符,单词,行,代码行,空行及可视化 Gitee项目地址:https://gitee.com/biubiubiuLYQ/word_and_character_statistics 一. ...
- Python实现百度贴吧自动顶贴机
开发这款小工具,我们需要做一些准备: url.txt:多个需要顶起的帖子地址. reply:多条随机回复的内容. selenium:浏览器自动化测试框架 首先,我们先使用pip完成selenium的安 ...
- 关于浏览器兼容问题——还有移动端meta问题
<!DOCTYPE html><!--[if lt IE 7]> <html dir="ltr" lang="en-US" cla ...