P3830 [SHOI2012]随机树 题解

P3830 随机树

坑题，别人的题解我看了一个下午没一个看得懂的，我还是太弱了。

题目链接 P3830 [SHOI2012]随机树

题目描述

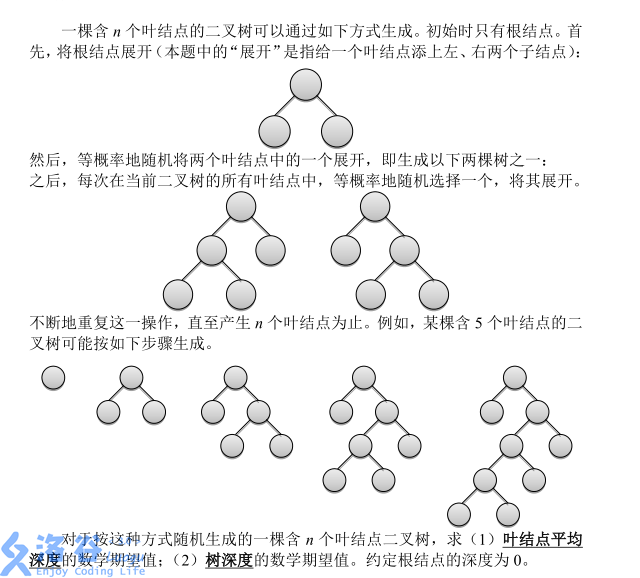
输入输出格式

输入格式：

输入仅有一行，包含两个正整数 q, n，分别表示问题编号以及叶结点的个数。

输出格式：

输出仅有一行，包含一个实数 d，四舍五入精确到小数点后 6 位。如果 q = 1，则 d 表示叶结点平均深度的数学期望值；如果 q = 2，则 d 表示树深度的数学期望值。

说明

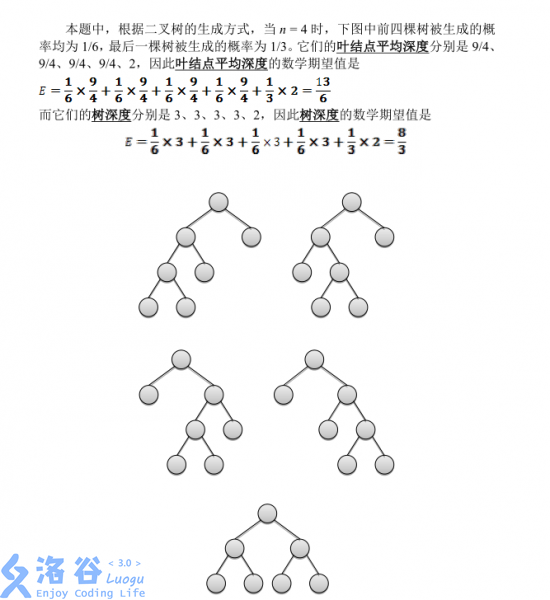
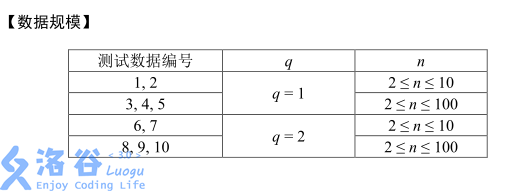
第一问很水，考虑每次新拓展节点就是让树的总深度加上 2

也就是: $$f[i]= \dfrac{f[i-1]*(i-1) + f[i-1] + 2 }{i}$$

意思就是原来 i-1 个节点的平均深度，乘上 (i-1) 变成深度和，然后再加一次 平均深度，然后加 2 ，除以 i 个叶子结点得到当前答案。

化简后式子就变成了: $$f[i]=f[i-1] + \dfrac{2} {i} $$

然后来到第二问（关键问题）。

首先这是概率期望 dp ，于是我们考虑设计状态。

那么我们让 $f[i][j]$ 表示 i 个叶子节点，深度为 j 的概率（是概率）。

那么转移就是： $$ f[i][j] = \dfrac{ f[k][j-1] + f[i-k][j-1]-f[k][j-1] \times f[i-k][j-1] } {i-1} $$

其中 f[i][j] 表示新树状态，f[k][j-1] 为左子树状态，f[i-k][j-1] 为右子树状态。

很多题解到这儿就没了，就没了！也不解释一下的说（尤其 i-1 解释的是真草率）。

最后我自己口胡了一下大概可能也许想通了。

首先 f[i][j] 是我们现在构造出的树的状态，也就是说我们用两个子树拼凑出了一棵新树，而根是新加节点（新加节点会使得左右子树所有叶子结点深度均增加 1 ）。

所以这点很重要，也是尤其关键的一步，在强调一遍，f[i][j] 只是代表了新树的形态，且是已经确定了的形态。

那么形成这棵树的概率也就是上面的转移式了，左子树有 j-1 个节点的概率 + 右子树有 j-1 个节点的概率 - 左右子树同时有 j-1 个节点的概率（容斥）。

接着呢？ 我们考虑除去 i-1 的意义（自己的想法而已）：

我们让当前的这棵树回到上一个状态，也就是说我们令这棵树最后一次叶子结点的扩展取消，回到 i-1 的状态。 （请脑补）

然后聪明的你已经想出来了，这时候要达到当前状态的概率是？ 当然是 1/(i-1) 。因为当前这棵树删除的节点扩展回来的概率就是 1/(i-1)。

然后问题就解决了，放代码（非常短啊）。

 //by Judge
 #include<iostream>
 #include<cstdio>
 using namespace std;
 int q,n; double ans,f[][];
 int main(){ scanf("%d%d",&q,&n);
     if(q==){
         for(int i=;i<=n;++i) ans+=2.0/i;
         return printf("%.6lf\n",ans),;
     } f[][]=f[][]=f[][]=;
     for(int i=;i<=n;++i) for(int j=;j<=n;++j)
         for(int k=;k<j;++k) for(int l=;l<i-j;++l)
             f[i][max(k,l)+]+=(f[j][k]*f[i-j][l])/(i-);
     for(int i=;i<n;++i) ans+=f[n][i]*i; return printf("%.6lf\n",ans),;
 }