二叉树翻转 · binary tree flipping

［抄题］：

给定一个二叉树，其中所有右节点要么是具有兄弟节点的叶节点(有一个共享相同父节点的左节点)或空白，将其倒置并将其转换为树，其中原来的右节点变为左叶子节点。返回新的根节点。

您在真实的面试中是否遇到过这个题？

Yes

样例

给出一个二叉树 {1,2,3,4,5}

    1
   / \
  2   3
 / \
4   5

返回二叉树的根 {4,5,2,#,#,3,1}

    4
   / \
  5   2
     / \
    3   1  

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

不知道怎么写dfs：先写总表达式bfs(某节点)，再写具体操作。实际执行是调用-调用-调用-调用……直到从最底端节点开始。

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

如果先翻转2，指向新节点后会失去和原左右节点的联系，导致断层。

如果先翻转6，没有左右节点，指向新节点后会失去和原左右节点的联系，也没关系。

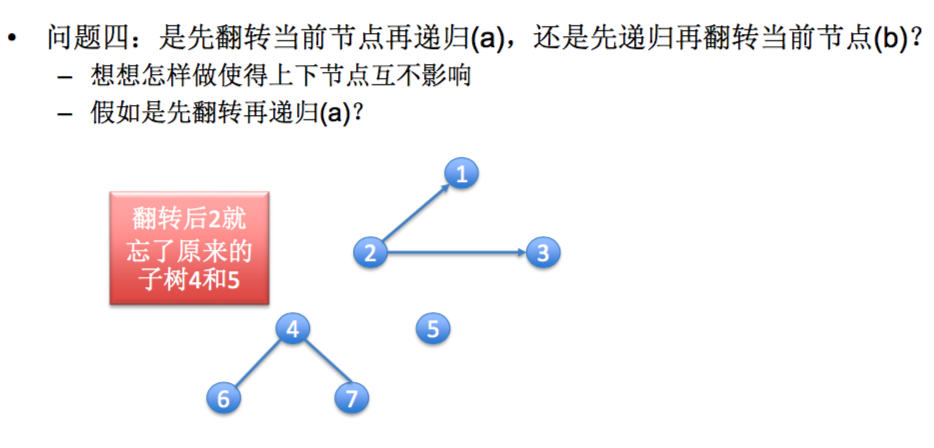
［一刷］：

1. bfs和主函数都要写各自的特判返回，bfs的特判和内容都是有继承关系的下一个点
2. 定义一个成员变量newroot，在void型bfs的特殊判断中发生联系

［二刷］：

1. 新树的左右是相反的，需要倒过来看。
2. 

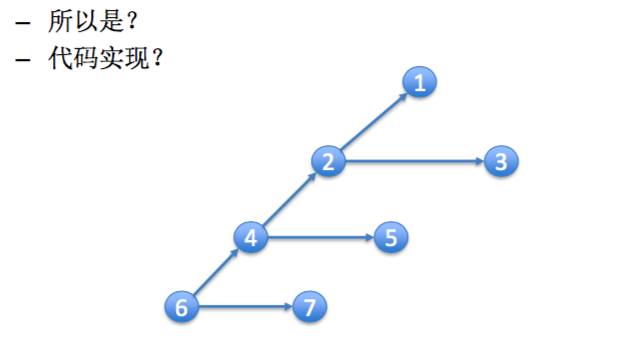
［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

就是用bfs再走一次

［复杂度］：Time complexity: O(n) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public class Solution {
    /*
     * @param root: the root of binary tree
     * @return: new root
     */
     TreeNode newRoot;
     //bfs
     //corner case
     void bfs(TreeNode curt) {
         if (curt.left == null) {
             newRoot = curt;
             return ;
         }
         bfs(curt.left);
         curt.left.right = curt;
         curt.left.left = curt.right;
         curt.left = null;
         curt.right = null;
     }

    public TreeNode upsideDownBinaryTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        bfs(root);
        return newRoot;
    }
}