SPOJ - PGCD Primes in GCD Table（莫比乌斯反演）

http://www.spoj.com/problems/PGCD/en/

题意：

给出a，b区间，求该区间内满足gcd(x,y)=质数的个数。

思路：

设f（n）为 gcd（x，y）=p的个数，那么F（n）为 p | gcd（x，y）的个数，显然可得F（n）=（x/p）*（y/p）。

这道题目因为可以是不同的质数，所以需要枚举质数，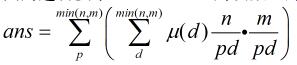

但是这样枚举太耗时，所以在这里令t=pk，

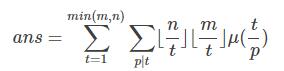
这样一来的话，我们只需要预处理u（t/p）的前缀和，之后像之前的题一样分块处理就可以了。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = 1e7 + ;

 int a, b;

 bool check[maxn];
 int prime[maxn];
 int mu[maxn];
 ll sum[maxn];

 void Mobius()
 {
     memset(check, false, sizeof(check));
     mu[] = ;
     int tot = ;
     for (int i = ; i <= maxn; i++)
     {
         if (!check[i])
         {
             prime[tot++] = i;
             mu[i] = -;
         }
         for (int j = ; j < tot; j++)
         {
             if (i * prime[j] > maxn)
             {
                 break;
             }
             check[i * prime[j]] = true;
             if (i % prime[j] == )
             {
                 mu[i * prime[j]] = ;
                 break;
             }
             else
             {
                 mu[i * prime[j]] = -mu[i];
             }
         }
     }

     sum[]=;
     for(int i=;i<tot;i++)
     {
         for(int j=prime[i];j<maxn;j+=prime[i])
         {
             sum[j]+=mu[j/prime[i]];
         }
     }
     for(int i=;i<maxn;i++)
         sum[i]+=sum[i-];
     return ;
 }

 ll solve(int n, int m)
 {
     if(n>m)  swap(n,m);
     ll ans=;

     for(int i=,last=;i<=n;i=last+)
     {
         last=min(n/(n/i),m/(m/i));
         ans+=(sum[last]-sum[i-])*(n/i)*(m/i);
     }
     return ans;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     int T;
     Mobius();

     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&a,&b);
         ll ans = solve(a,b);
         printf("%lld\n",ans);
     }
     return ;
 }