支持向量机SVM——专治线性不可分
SVM原理
线性可分与线性不可分
线性可分
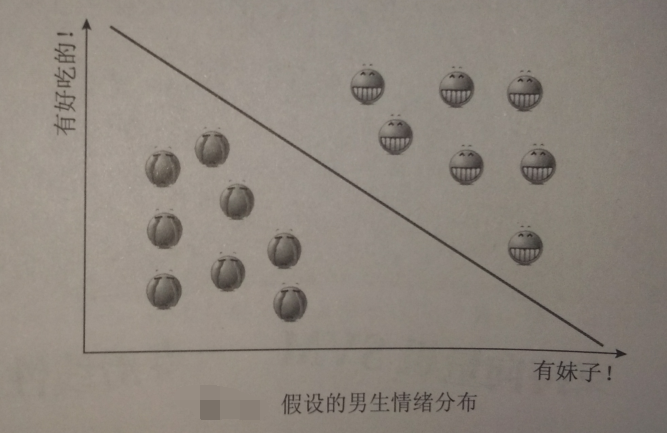
线性不可分-------【无论用哪条直线都无法将女生情绪正确分类】
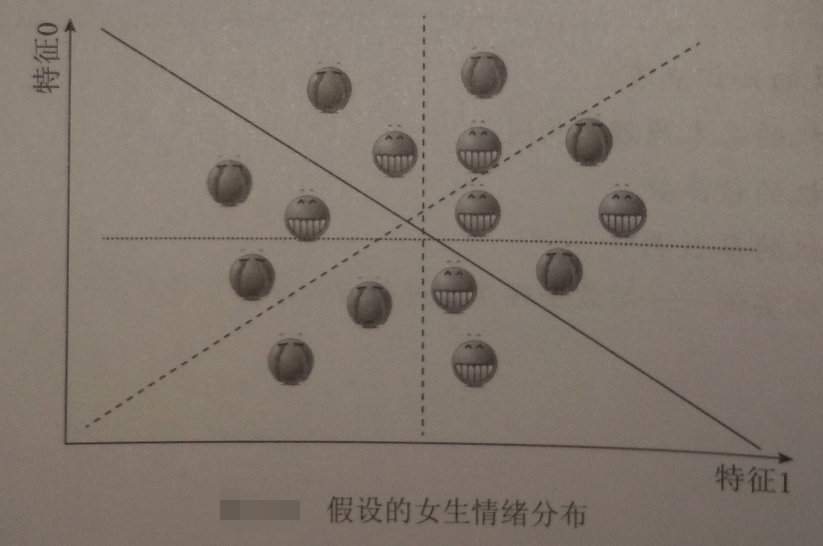
SVM的核函数可以帮助我们:
假设‘开心’是轻飘飘的,“不开心”是沉重的
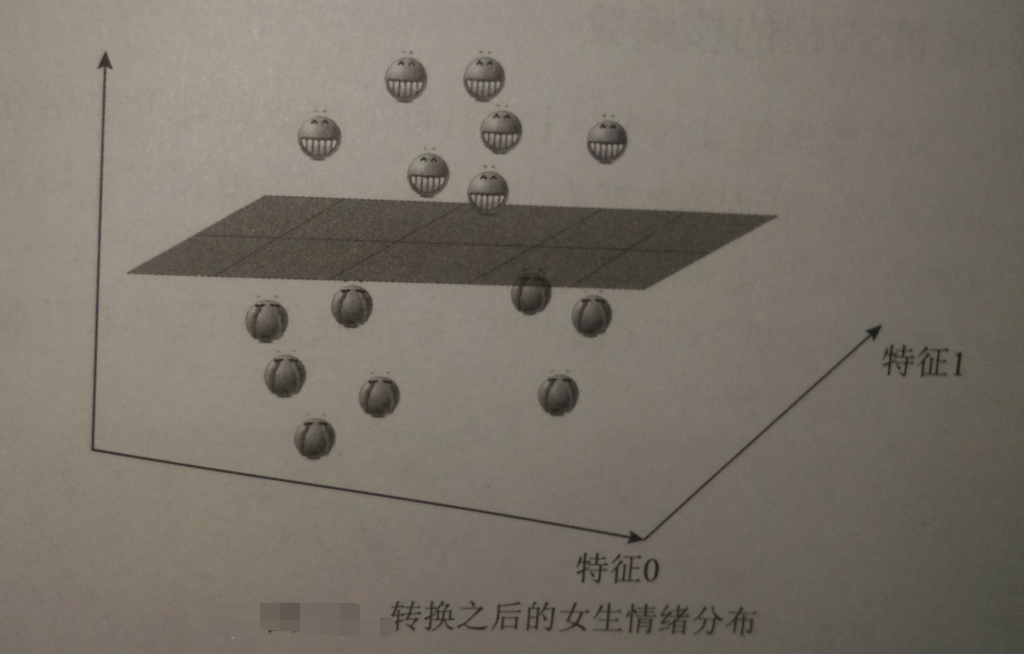
将三维视图还原成二维:
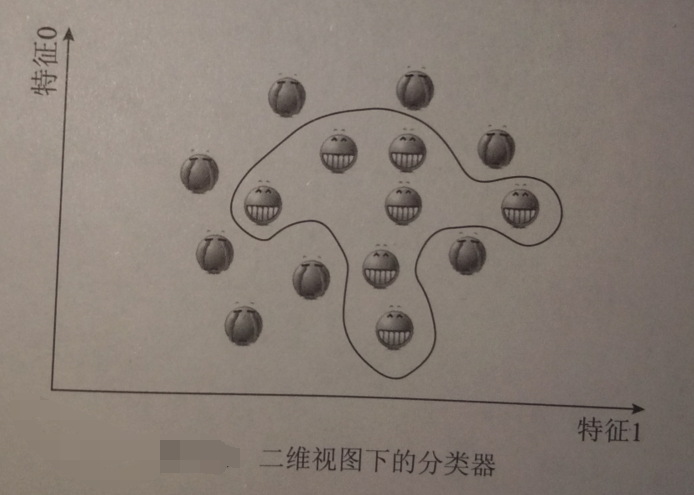
刚利用“开心”“不开心”的重量差实现将二维数据变成三维的过程,称为将数据投射至高维空间,这正是核函数的功能
在SVM中,用的最普遍的两种把数据投射到高维空间的方法分别是多项式内核、径向基内核(RFB)
多项式内核:
通过把样本原始特征进行乘方来把数据投射到高维空间【如特征1^2,特征2^3,特征3^5......】
RBF:
又称高斯内核
支持向量机的SVM核函数

用图形直观了解:
#导入numpy
import numpy as np
#导入画图工具
import matplotlib.pyplot as plt
#导入支持向量机SVM
from sklearn import svm
#导入数据集生成工具
from sklearn.datasets import make_blobs
#先创建50个数据点,让它们分成两类
X,y = make_blobs(n_samples=50,centers=2,random_state = 6)
#创建一个线性内核的支持向量机模型
clf = svm.SVC(kernel = 'linear',C=1000)
clf.fit(X,y)
#把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#生成两个等差数列
xx = np.linspace(xlim[0],xlim[1],30)
yy = np.linspace(ylim[0],ylim[1],30)
YY,XX = np.meshgrid(yy,xx)
xy = np.vstack([XX.ravel(),YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
#把分类的边界画出来
ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100,linewidth=1,facecolors='none')
plt.show()
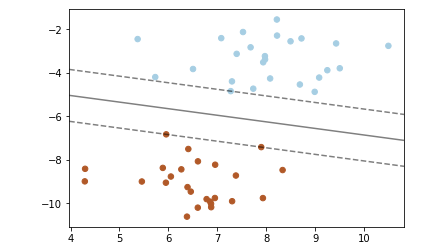 ——线性内核的SVM分类器
——线性内核的SVM分类器
【结果分析】:
在分类器两侧有两条虚线,正好压在虚线上的数据点,即支持向量
本例所使用的方法称为“最大边界间隔超平面”
指,实线【在高维数据中是一个超平面】和所有支持向量的距离都是最大的
把SVM的内核换成RBF:
#创建一个RBF内核的支持向量机模型
clf_rbf = svm.SVC(kernel='rbf',C=1000)
clf_rbf.fit(X,y)
#把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#生成两个等差数列
xx = np.linspace(xlim[0],xlim[1],30)
yy = np.linspace(ylim[0],ylim[1],30)
YY,XX = np.meshgrid(yy,xx)
xy = np.vstack([XX.ravel(),YY.ravel()]).T
Z = clf_rbf.decision_function(xy).reshape(XX.shape)
#把分类的边界画出来
ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
ax.scatter(clf_rbf.support_vectors_[:,0],clf_rbf.support_vectors_[:,1],s=100,linewidth=1,facecolors='none')
plt.show()
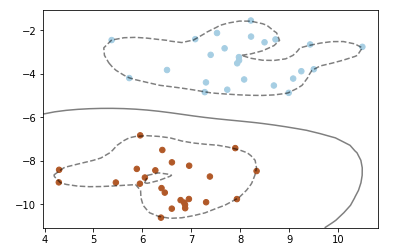 ——RBF内核的SVM分类器
——RBF内核的SVM分类器
【结果分析】:
使用RBF内核时,数据点距离计算是用如下公式计算的:
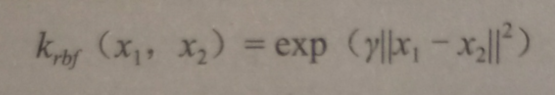

SVM的核函数和参数选择
1.不同核函数的SVM对比
线性模型中提到过,linearSVM算法,就是一种使用了线性内核的SVM算法,不过linearSVM不支持对核函数进行修改【默认只能使用线性内核】
直观体验不同内核的SVM算法在分类中的不同表现:
from sklearn.datasets import load_wine
#定义一个函数来画图
def make_meshgrid(x,y,h=.02):
x_min,x_max = x.min() -1,x.max() +1
y_min,y_max = y.min() -1,y.max() +1
xx,yy = np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
return xx,yy
#定义一个绘制等高线的函数
def plot_contours(ax,clf,xx,yy, **params):
Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx,yy,Z, **params)
return out
#使用酒的数据集
wine = load_wine()
#选取数据集的前两个特征
X = wine.data[:,:2]
y = wine.target
C = 1.0 #SVM的正则化参数
models = (clf.fit(X,y) for clf in models)
#设定图题
titles = ('SVC with linear kernal','LinearSVC (linear kernal)','SVC with RBF kernal','SVC with polynomial (degree 3) kernal')
#设定一个子图形的个数和排列方式
fig,sub = plt.subplots(2,2)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
#使用前面定义的函数进行画图
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors='k')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
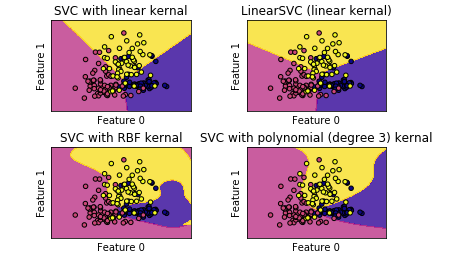
【结果分析】:
线性内核的SVC与linearSVC得到的结果近似,但仍然有一点差别——原因是linearSVC对L2范数进行最小化,而线性内核的SVC是对L1进行最小化
无论如何,线性内核的SVC和linearSVC生成的决定边界都是线性的【在更高维数据集中将会是相交的超平面】
RBF内核的SVC和polynomial内核的SVC分类器的决定边界则完全不是线性的,更加弹性
决定他们边界形状的是参数:
polynomial内核的SVC分类器
degree和正则化参数C
【本例中degree=3,即对原始数据集的特征乘3次方操作】
RBF内核的SVC
gamma和正则化参数C
RBF内核SVC的gamma参数调节
models = (clf.fit(X,y) for clf in models)
#设定图题
titles = ('gamma=0.1','gamma=1','gamma=10')
#设置子图形个数和排列
flg,sub = plt.subplots(1,3,figsize=(10,3))
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors='k')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
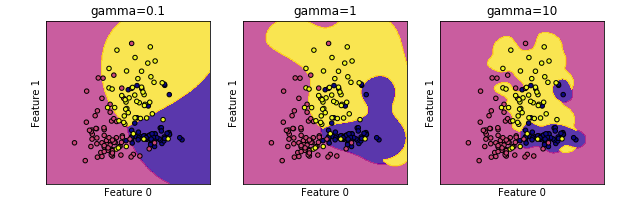
【结果分析】:
gamma值越小,RBF内核的直径越大——> 有更多的点被模型圈进决定边界中——> 边界越圆滑
- gamma越小,模型倾向于 欠拟合
- gamma越大,模型倾向于 过拟合
正则化参数C,可以见线性模型一章
- C越小,模型越受限【单个数据对模型的影响越小】,模型越简单
- C越大,每个数据点对模型的影响越大,模型越复杂
SVM优点
- 可应对高维数据集和低维数据集
- 即使数据集中样本特征的测度都比较接近,如图像识别领域,以及样本特征数和样本数比较接近的时候,都游刃有余
SVM缺点
- 当数据集中特征数量在1万以内,SVM可以驾驭,但数量大于10万,就非常占内存和耗费时间
- 对数据预处理和参数调节要求很高
【注意】
SVM中3个参数非常重要:
- 核函数的选择
- 核函数的参数【如RBF的gamma】
- 正则化参数C
RBF内核的gamma值是用来调节内核宽度的,gamma值和C值一起控制模型的复杂度,数值越大,模型越复杂【实际中,一起调节,才能达到最好的效果】
实战
SVM在回归分析中的应用——波士顿房价数据集
1.了解数据集
#导入波士顿房价
from sklearn.datasets import load_boston
boston = load_boston()
#打印键
print(boston.keys())
#打印数据集中的短描述
print(boston['DESCR'])

【一部分】
【结果分析】
数据集共有506个样本,每个样本有13个特征变量,后面还有一个叫做中位数的第14个变量【这变量就是该数据集中的target】
2.通过SVR算法建立房价预测模型
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
#建立数据集和测试集
X,y = boston.data,boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
#打印训练集和测试集的形态
print(X_train.shape)
print(X_test.shape)

用SVR建模
#导入支持向量回归模型
from sklearn.svm import SVR
#分别测试linear核函数和rbf核函数
for kernel in ['linear','rbf']:
svr = SVR(kernel=kernel)
svr.fit(X_train,y_train)
print(kernel,'核函数模型训练集得分:',svr.score(X_train,y_train))
print(kernel,'核函数模型测试集得分:',svr.score(X_test,y_test))

SVM算法对数据预处理的要求较大,如果 数据特征量级差异较大 ,就需要预处理数据
先用图形可视化:
#将特征数值中的min和max用散点图画出来
plt.plot(X.min(axis=0),'v',label='min')
plt.plot(X.max(axis=0),'^',label='max')
#设定纵坐标为对数形式
plt.yscale('log')
#设定图注位置最佳
plt.legend(loc='best')
plt.xlabel('features')
plt.ylabel('feature magnitude')
plt.show()
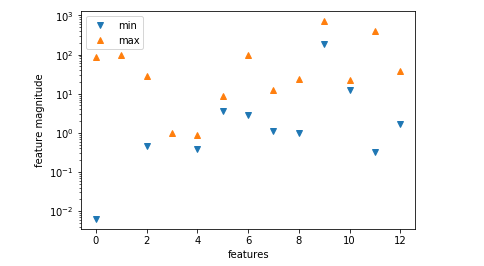
显然,量级差异较大
预处理:
from sklearn.preprocessing import StandardScaler
#预处理
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
#将预处理后的数据特征的max和min用散点图表示出来
plt.plot(X_train_scaled.min(axis=0),'v',label='train set min')
plt.plot(X_train_scaled.max(axis=0),'^',label='train set max')
plt.plot(X_test_scaled.min(axis=0),'v',label='test set min')
plt.plot(X_test_scaled.max(axis=0),'^',label='test set max')
plt.legend(loc='best')
plt.xlabel('scaled features')
plt.ylabel('scaled feature magnitude')
plt.show()
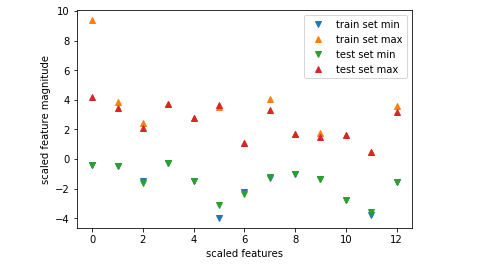
【结果分析】
经过预处理,无论训练集还是测试集,所有特征的最大值不会超过10,最小值趋近0,以至图中看不到
用预处理的数据训练模型:
#使用预处理后的数据重新训练模型
for kernel in ['linear','rbf']:
svr = SVR(kernel=kernel)
svr.fit(X_train_scaled,y_train)
print(kernel,'训练集得分:',svr.score(X_train_scaled,y_train))
print(kernel,'测试集得分:',svr.score(X_test_scaled,y_test))

进一步调整参数
#设置模型的C参数和gamma参数
svr = SVR(C=100,gamma=0.1)
svr.fit(X_train_scaled,y_train)
print('训练集得分:',svr.score(X_train_scaled,y_train))
print('测试集得分:',svr.score(X_test_scaled,y_test))
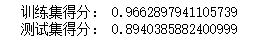
支持向量机SVM——专治线性不可分的更多相关文章
- 支持向量机(SVM)的推导(线性SVM、软间隔SVM、Kernel Trick)
线性可分支持向量机 给定线性可分的训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习到的分离超平面为 \[w^{\ast }x+b^{\ast }=0\] 以及相应的决策函数 \[f\le ...
- SVM之解决线性不可分
SVM之问题形式化 SVM之对偶问题 SVM之核函数 >>>SVM之解决线性不可分 写在SVM之前——凸优化与对偶问题 上一篇SVM之核函数介绍了通过计算样本核函数,实际上将样本映射 ...
- 支持向量机SVM 参数选择
http://ju.outofmemory.cn/entry/119152 http://www.cnblogs.com/zhizhan/p/4412343.html 支持向量机SVM是从线性可分情况 ...
- opencv 支持向量机SVM分类器
支持向量机SVM是从线性可分情况下的最优分类面提出的.所谓最优分类,就是要求分类线不但能够将两类无错误的分开,而且两类之间的分类间隔最大,前者是保证经验风险最小(为0),而通过后面的讨论我们看到,使分 ...
- 支持向量机SVM、优化问题、核函数
1.介绍 它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解. 2.求解过程 1.数据分类—SVM引入 ...
- OpenCV支持向量机SVM对线性不可分数据的处理
支持向量机对线性不可分数据的处理 目标 本文档尝试解答如下问题: 在训练数据线性不可分时,如何定义此情形下支持向量机的最优化问题. 如何设置 CvSVMParams 中的参数来解决此类问题. 动机 为 ...
- 线性可分支持向量机--SVM(1)
线性可分支持向量机--SVM (1) 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 线性可分支持向量机的定义: ...
- 统计学习:线性支持向量机(SVM)
学习策略 软间隔最大化 上一章我们所定义的"线性可分支持向量机"要求训练数据是线性可分的.然而在实际中,训练数据往往包括异常值(outlier),故而常是线性不可分的.这就要求我们 ...
- [白话解析] 深入浅出支持向量机(SVM)之核函数
[白话解析] 深入浅出支持向量机(SVM)之核函数 0x00 摘要 本文在少用数学公式的情况下,尽量仅依靠感性直觉的思考来讲解支持向量机中的核函数概念,并且给大家虚构了一个水浒传的例子来做进一步的通俗 ...
随机推荐
- html中的meta标签是什么?有哪些属性?
meta标签介绍 meta标签是HTML语言head区域的一个辅助性标签,常用于定义页面的说明,关键字,最后修改的日期和其他的元数据.这些元数据将服务于浏览器,搜索引擎和其他网络服务. meta标签的 ...
- zoj 3605
链接 [https://vjudge.net/contest/293343#problem/F] 题意 就是有n碗,有一个宝石,知道开始宝石在那个碗下面 进行M次交换,但知道其中的k次,问你最可能在那 ...
- Divide Candies CodeForces - 1056B (数学)
Arkady and his friends love playing checkers on an n×nn×n field. The rows and the columns of the fie ...
- Python之shutil模块(复制移动文件)
用python实现将某代码文件复制/移动到指定路径下.场景例如:mv ./xxx/git/project1/test.sh ./xxx/tmp/tmp/1/test.sh (相对路径./xxx/tmp ...
- spring整合quartz异常:org.quartz.JobPersistenceException: Couldn't clean volatile data: Unknown column 'IS_VOLATILE' in 'where clause'
自己的SSM项目中要用到定时器,初期使用Timer,后来用spring 的schedule,都比较简单,所以功能比较单一.后来就研究quartz,准备整合到项目中.遇到了异常,异常内容如下: [201 ...
- Python——模块——配置模块(ConfigParser)
一.读取 read(filename) 直接读取ini文件内容 sections() 得到所有的section,并以列表的形式返回 options(section) 得到该section的所有opt ...
- Spring Boot整合Elasticsearch
Spring Boot整合Elasticsearch Elasticsearch是一个全文搜索引擎,专门用于处理大型数据集.根据描述,自然而然使用它来存储和搜索应用程序日志.与Logstash和K ...
- Security+ 认证考过经验分享 802分飘过
PART 1/考前准备 1.针对与新人.学生建议看每一节直播课程,老师会结合自己的工作工作经验讲解课程,可以帮助学生理解知识. 2.备考期间建议官方指导手册至少看两遍以上,我在结合自己的做题库时发现有 ...
- (N叉树 递归) leetcode589. N-ary Tree Preorder Traversal
Given an n-ary tree, return the preorder traversal of its nodes' values. For example, given a 3-ary ...
- boto3库限速
# -*- coding: utf-8 -*- import boto3 from boto3.s3.transfer import TransferConfig # from s3transfer. ...
