AI之旅（7）：神经网络之反向传播

前置知识

  求导

知识地图

  神经网络算法是通过前向传播求代价，反向传播求梯度。在上一篇中介绍了神经网络的组织结构，逻辑关系和代价函数。本篇将介绍如何求代价函数的偏导数（梯度）。

梯度检测

  在进入主题之前，先了解一种判断代价函数的求导结果是否正确的方法，这种方法称为梯度检测。现在假设我们已经掌握了反向传播，可以计算出代价函数的偏导数。

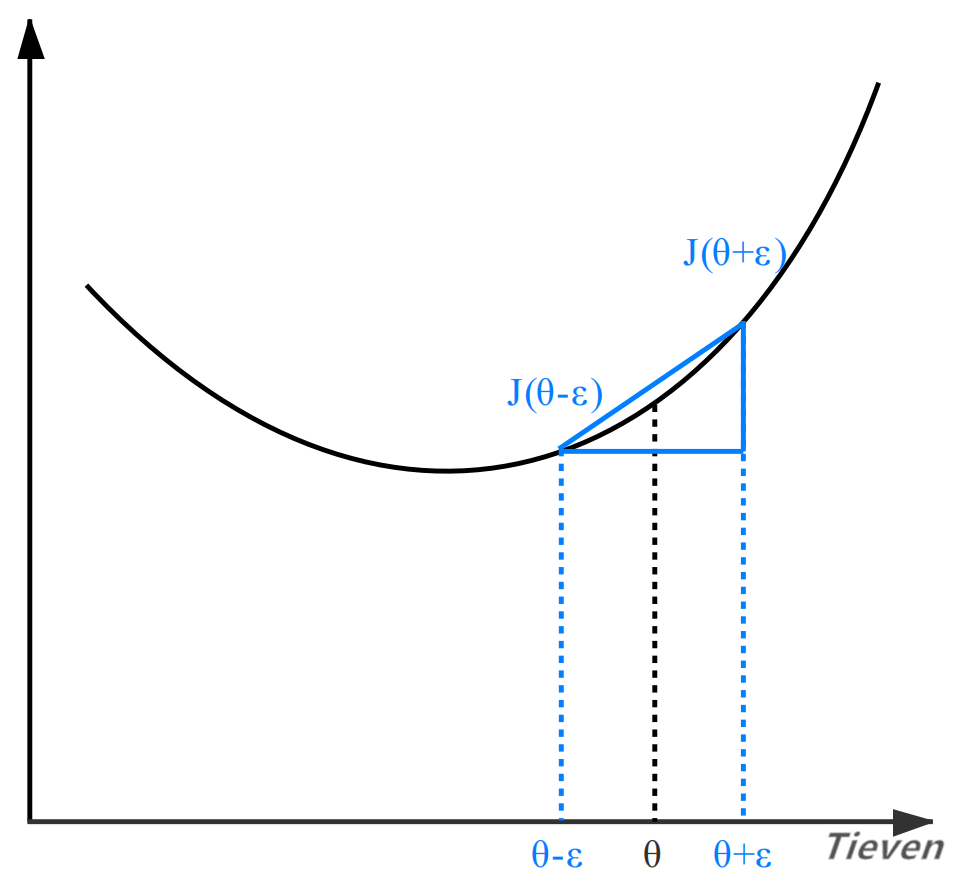
  当函数只有一个变量时，已知导数是切线的斜率，如果能求出某个点的斜率，也就求出了该点的导数。当ε足够小时（如10的-4次方），θ处的斜率可以近似表示为如下形式：

  这是斜率的近似值，同时它也是导数的近似值。在求导方法正确的情况下，通过算法得到的导数与梯度检测得到的导数，两者之间的误差应该非常小（如10的-9次方）。

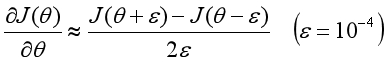
  同理，当函数有多个变量时对应有多个偏导数。通过将其他变量视为常数，可以用相同的方法得到每一个偏导数的近似值，进而得到整个偏导数向量的近似值。

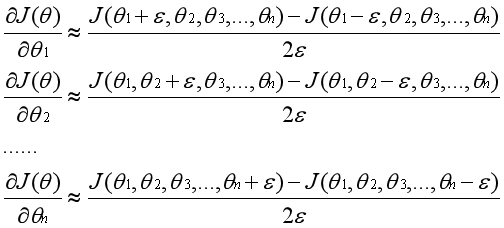
模型与概念

  延用上一篇的例子，这是一个总共4层，每层都由激活项组成，含有偏置单元的神经网络模型。第一层为输入层，第二、三层为隐藏层，第四层为输出层，对应有3个参数矩阵。

  激活项：每一层的激活项等于前一层的激活项经过线性组合，作用于激活函数的值。特别约定用特征作为第一层的激活项。

  激活函数：这里使用Sigmoid函数作为激活函数，这并不是最适合神经网络的激活函数，神经网络也支持其他的激活函数。

  偏置单元：偏置单元是值等于1的特殊的激活项，用虚线表示。每层的偏置单元与前一层没有联系，只用于后一层的使用。

  输入层：样本的特征为输入层，第一个特征不是原始特征，是手动添加的值为1的元素，因此刚好与偏置单元相对应。

  隐藏层：隐藏层也是由激活项组成，隐藏层中激活项的数量没有限制，隐藏层的总层数也没有限制，这些都可以自定义。

  输出层：预测的结果为输出层，模型需要识别几种分类，输出层就有几个激活项，激活项的值表示样本属于该类别的概率。

  参数矩阵：在逻辑回归中参数是向量的形式，在神经网络中参数是矩阵的形式，有n层神经网络对应的有n-1个参数矩阵。

前向传播

  通过第一个参数矩阵，从第一层激活项获得第二层激活项，为第二层激活项添加偏置单元：

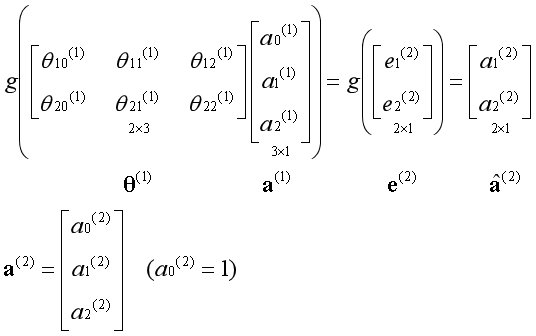
  为了方便后续讲述，添加一个中间变量e，e的值为如下形式：

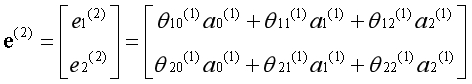
  通过第二个参数矩阵，从第二层激活项获得第三层激活项，为第三层激活项添加偏置单元：

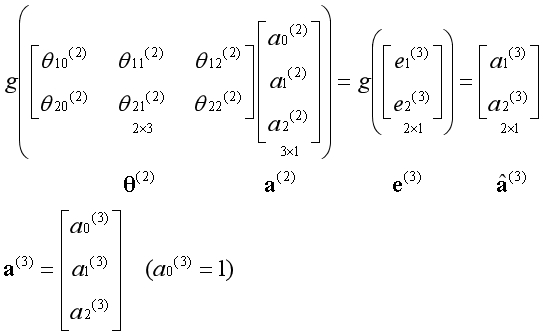
  通过第三个参数矩阵，从第三层激活项获得第四层激活项，第四层激活项为预测结果，预测结果不添加偏置单元：

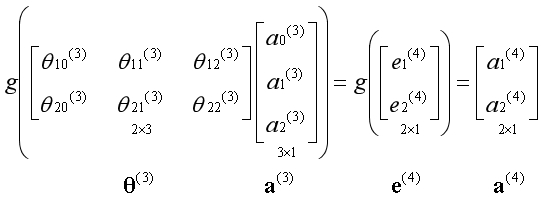
  通过前向传播得到预测结果，根据激活函数的性质，可以构建出神经网络的代价函数。虽然形式上比较复杂，神经网络的代价函数本质上与逻辑回归的代价函数一致。

  全部样本的偏导数可以视为每个样本的偏导数的累加，因此只需关注如何对一个样本的代价函数求导，同时暂时不考虑正则项部分。将代价函数展开，所包含的元素如下：

  观察元素之间的对应关系，从上往下看，激活项通过层层压缩得到预测结果。从下往上看，预测结果通过层层展开得到激活项。使用链式法则可以求出每一个具体的偏导数。

链式法则：符号约定

  在神经网络中参数是矩阵的形式，对应的偏导数也是矩阵的形式。因此在了解如何用链式法则求具体的偏导数之后，还需要寻找到一种方法可以直接求出偏导数矩阵。

  定义不含偏置单元的激活项向量为如下形式：

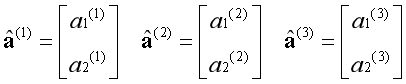
  定义对应的参数矩阵为如下形式：

  定义矩阵点乘符号为如下形式：

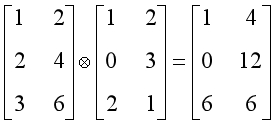
链式法则：基本原理

  原理1：函数中任何元素都可视为变量，当函数对变量求导时，将其他元素视为常数。

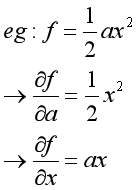
  原理2：两个函数和的导数等于这两个函数导数的和。

  注：观察代价函数可以发现，前一层的激活项在后一层的所有激活项中都有出现（除偏置单元）。

误差项：第四层

  代价函数对第4层的中间变量求导，求导的结果称为第4层的误差项，根据链式法则等于如下形式：

  代价函数对第3层的参数求导，根据链式法则等于如下形式：

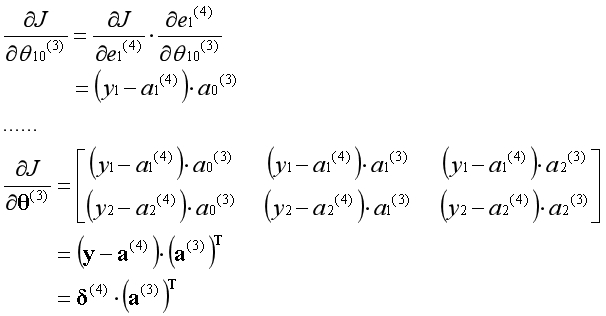
  代价函数对第3层的激活项（除偏置单元）求导，根据链式法则等于如下形式：

  我们发现对单个元素求导需要写很长的公式，对整个向量或矩阵求导反而可以写得很简洁。现在还看不出偏导数矩阵之间存在的规律，根据链式法则继续求第二个偏导数矩阵。

误差项：第三层

  代价函数对第3层的中间变量求导，求导的结果称为第3层的误差项，根据链式法则等于如下形式：

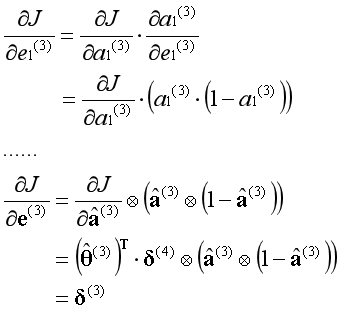
  代价函数对第2层的参数求导，根据链式法则等于如下形式：

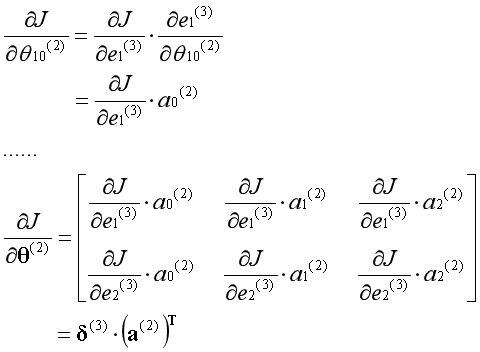
  代价函数对第2层的激活项（除偏置单元）求导，根据链式法则等于如下形式：

误差项：第二层

  代价函数对第2层的中间变量求导，求导的结果称为第2层的误差项，根据链式法则等于如下形式：

  代价函数对第1层的参数求导，根据链式法则等于如下形式：

  对第k层激活项（除偏置单元）求导，是为了求出第k层的误差项。求第k层误差项，是为了求出第k-1个偏导数矩阵。因此只需求出第2层误差项即可得到第1个偏导数矩阵。

误差项：总览

  观察每一层的误差项和每一个偏导数矩阵，会发现误差项与误差项，误差项与偏导数矩阵之间存在明显的规律性。其中红色方框为第K层，蓝色方框为第K-1层至第2层。

  偏导数矩阵可由误差项求出，前一层的误差项又可通过后一层的误差项求出，除了最后一层的误差项外，其他层的误差项遵循统一的形式。这是反向传播的核心部分。

正则项部分的偏导数

  代价函数中的正则项部分如下：

  正则项对应的偏导数矩阵如下：

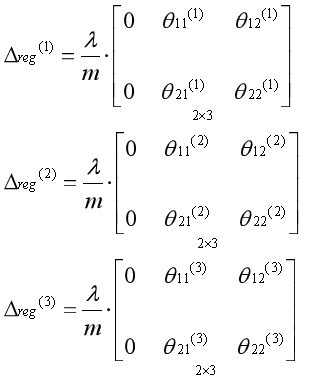
  什么时候添加正则项对应的偏导数矩阵？当计算出代价函数第一部分对应的偏导数矩阵后，再累加上正则项部分对应的偏导数矩阵。现在可以总结出完整的反向传播算法。

算法

向量化

  根据上面的算法可以写出每次使用一个样本训练的神经网络模型，但是使用循环还是太慢了。通过对上述算法进行小小改动，我们可以得到支持批量样本训练的模型。

  矩阵可以和向量进行运算，矩阵也可以和矩阵进行运算。用转置的样本矩阵X替换单个向量x，用转置的标签矩阵Y替换单个向量y，即可省略循环语句提升计算速度。

总结

  神经网络算法的核心，是理解如何使用链式法则求单个偏导数。通过观察偏导数矩阵的形式，总结出通过误差项直接求偏导数矩阵的方法。最后对算法进行改进实现向量化计算。

  至此我们构建了一个具有多重隐藏层，含有偏置单元，支持向量化计算的深度神经网络模型。既然能够计算出模型的代价和梯度，就可以使用梯度上升法或者高级优化方法求解。

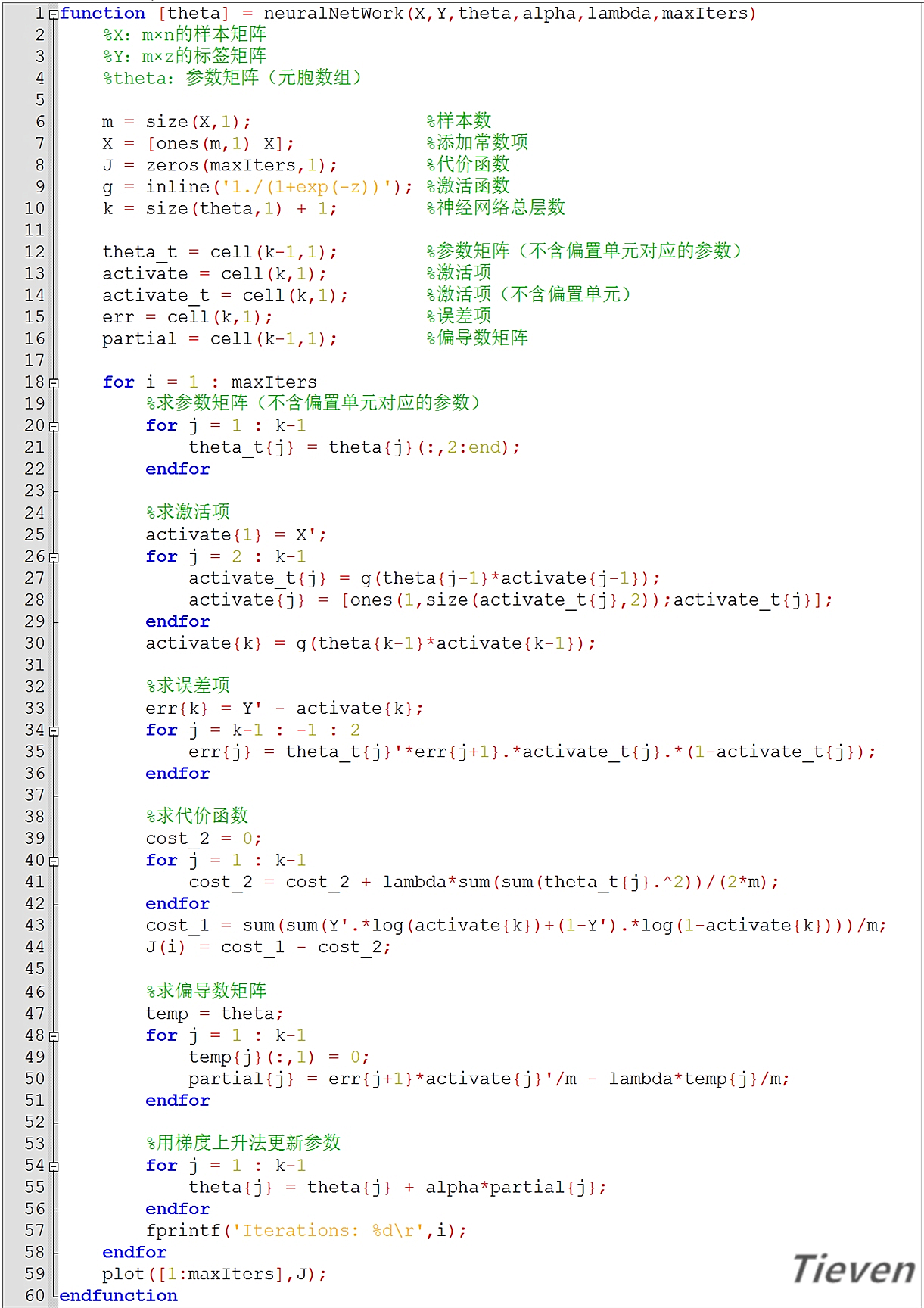
非正规代码

版权声明

  1，本文为原创文章，未经作者授权禁止引用、复制、转载、摘编。

  2，对于有上述行为者，作者将保留追究其法律责任的权利。

Tieven

2019.1.16

tieven.it@gmail.com