P2542 [AHOI2005]航线规划 LCT维护双连通分量

$\color{#0066ff}{ 题目描述 }$

对Samuel星球的探险已经取得了非常巨大的成就，于是科学家们将目光投向了Samuel星球所在的星系——一个巨大的由千百万星球构成的Samuel星系。

星际空间站的Samuel II巨型计算机经过长期探测，已经锁定了Samuel星系中许多星球的空间坐标，并对这些星球从1开始编号1、2、3……。

一些先遣飞船已经出发，在星球之间开辟探险航线。

探险航线是双向的，例如从1号星球到3号星球开辟探险航线，那么从3号星球到1号星球也可以使用这条航线。

例如下图所示：

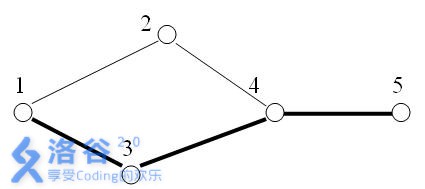
在5个星球之间，有5条探险航线。

A、B两星球之间，如果某条航线不存在，就无法从A星球抵达B星球，我们则称这条航线为关键航线。

显然上图中，1号与5号星球之间的关键航线有1条：即为4-5航线。

然而，在宇宙中一些未知的磁暴和行星的冲撞，使得已有的某些航线被破坏，随着越来越多的航线被破坏，探险飞船又不能及时回复这些航线，可见两个星球之间的关键航线会越来越多。

假设在上图中，航线4-2（从4号星球到2号星球）被破坏。此时，1号与5号星球之间的关键航线就有3条：1-3，3-4，4-5。

小联的任务是，不断关注航线被破坏的情况，并随时给出两个星球之间的关键航线数目。现在请你帮助完成。

$\color{#0066ff}{输入格式}$

第一行有两个整数N，M。表示有N个星球（1< N < 30000），初始时已经有M条航线（1 < M < 100000）。随后有M行，每行有两个不相同的整数A、B表示在星球A与B之间存在一条航线。接下来每行有三个整数C、A、B。C为1表示询问当前星球A和星球B之间有多少条关键航线；C为0表示在星球A和星球B之间的航线被破坏，当后面再遇到C为1的情况时，表示询问航线被破坏后，关键路径的情况，且航线破坏后不可恢复； C为-1表示输入文件结束，这时该行没有A,B的值。被破坏的航线数目与询问的次数总和不超过40000。

$\color{#0066ff}{输出格式}$

对每个C为1的询问，输出一行一个整数表示关键航线数目。

$\color{#0066ff}{输入样例}$

$\color{#0066ff}{输出样例}$

1

3

$\color{#0066ff}{数据范围与提示}$

我们保证无论航线如何被破坏，任意时刻任意两个星球都能够相互到达。在整个数据中，任意两个星球之间最多只可能存在一条直接的航线。

$\color{#0066ff}{ 题解 }$

正序删边我们不好维护这种东西，考虑离线倒序加边

一旦出现环，我们就暴力缩点，用ufs来维护所属的双连通分量

显然树链上每个点代表一个双连通分量，那么答案就是点数- 1

在连边的时候，如果不成环，直接连即可，如果成环，暴力dfs把所有点的ufs的父亲设为当前点

那它们原来的父亲不就无效了吗，所以access的时候，把父亲设为ufs的父亲即可

#include<bits/stdc++.h>

#define LL long long

LL in() {

	char ch; LL x = 0, f = 1;

	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);

	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));

	return x * f;

}

const int maxn = 3e4 + 9;

const int maxm = 1e5 + 9;

struct node {

	node *ch[2], *fa;

	int siz, rev;

	node(int siz = 1, int rev = 0): siz(siz), rev(rev) { ch[0] = ch[1] = fa = NULL; }

	void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }

	void upd() {

		siz = 1;

		if(ch[0]) siz += ch[0]->siz;

		if(ch[1]) siz += ch[1]->siz;

	}

	void dwn() {

		if(!rev) return;

		if(ch[0]) ch[0]->trn();

		if(ch[1]) ch[1]->trn();

		rev = 0;

	}

	bool ntr() { return fa && (fa->ch[0] == this || fa->ch[1] == this); }

	bool isr() { return fa->ch[1] == this; }

}pool[maxn];

int fa[maxn];

void rot(node *x) {

	node *y = x->fa, *z = y->fa;

	bool k = x->isr(); node *w = x->ch[!k];

	if(y->ntr()) z->ch[y->isr()] = x;

	(x->ch[!k] = y)->ch[k] = w;

	(y->fa = x)->fa = z;

	if(w) w->fa = y;

	y->upd(), x->upd();

}

void splay(node *o) {

	static node *st[maxn];

	int top;

	st[top = 1] = o;

	while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;

	while(top) st[top--]->dwn();

	while(o->ntr()) {

		if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);

		rot(o);

	}

}

int findset(int x) { return x == fa[x]? fa[x] : fa[x] = findset(fa[x]); }

void access(node *x) {

	for(node *y = NULL; x;) {

		splay(x), x->ch[1] = y, x->upd();

		y = x;

		if(x->fa) x = x->fa = pool + findset(x->fa - pool);

		else x = x->fa;

	}

}

void makeroot(node *o) { access(o), splay(o), o->trn(); }

node *findroot(node *o) {

	access(o), splay(o);

	while(o->dwn(), o->ch[0]) o = o->ch[0];

	return splay(o), o;

}

void del(node *o, int f) { if(o) fa[o - pool] = f, del(o->ch[0], f), del(o->ch[1], f); }

void out();

void link(int l, int r) {

	if(l == r) return;

	node *x = pool + l, *y = pool + r;

	makeroot(x);

	if(findroot(y) != x) return (void)(x->fa = y);

	del(x->ch[1], x - pool);

	if(x->ch[1]) x->ch[1] = NULL;

	x->upd();

}

int query(int l, int r) {

	node *x = pool + l, *y = pool + r;

	makeroot(x), access(y), splay(y);

	return y->siz - 1;

}

using std::pair;

using std::make_pair;

pair<int, int> e[maxm], q[maxm];

std::map<pair<int, int>, int> mp;

bool vis[maxm];

int id[maxm], n, m, ans[maxn];

int main() {

	n = in(), m = in();

	int x, y;

	for(int i = 1; i <= n; i++) fa[i] = i;

	for(int i = 1; i <= m; i++) {

		x = in(), y = in();

		if(x > y) std::swap(x, y);

		mp[e[i] = make_pair(x, y)] = i;

	}

	int num = 0;

	while(~(id[++num] = in())) {

		x = in(), y = in();

		if(x > y) std::swap(x, y);

		q[num] = make_pair(x, y);

		if(id[num] == 0) vis[mp[q[num]]] = true;

	}

	for(int i = 1; i <= m; i++) if(!vis[i]) link(findset(e[i].first), findset(e[i].second));

	int v = 0;

	for(int i = num - 1; i >= 1; i--) {

		x = findset(q[i].first), y = findset(q[i].second);

		if(id[i] == 1) ans[++v] = query(x, y);

		else link(x, y);

	}

	for(int i = v; i >= 1; i--) printf("%d\n", ans[i]);

	return 0;

}