POJ 3347 Kadj Squares

Kadj Squares

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 2132		Accepted: 843

Description

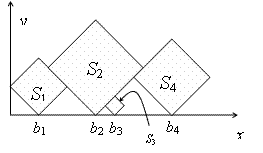
In this problem, you are given a sequence S₁, S₂, ..., S_n of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let b_i be the x coordinates of the bottom vertex of S_i. First, put S₁ such that its left vertex lies on x=0. Then, put S₁, (i > 1) at minimum b_i such that

• b_i > b_i-1 and
• the interior of S_i does not have intersection with the interior of S₁...S_i-1.

The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S₁, S₂, and S₄ have this property. More formally, S_i is visible from above if it contains a point p, such that no square other than S_i intersect the vertical half-line drawn from p upwards.

Input

The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of S_i. The input is terminated by a line containing a zero number.

Output

For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.

Sample Input

4
3 5 1 4
3
2 1 2
0

Sample Output

1 2 4
1 3

Source

Tehran 2006

 

 

 

 

 

这题是在做计算几何的时候遇到的。

 

但是发现有简单的做法，不需要用计算几何。

 

为了避免浮点数运算，把长度乘以sqrt(2).

 

具体看代码吧，代码看得很清楚了。

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;

const int MAXN = ;
struct Node
{
    int l,r,len;
};
Node node[MAXN];
int main()
{
    int n;
    while(scanf("%d",&n) ==  && n)
    {
        for(int i = ;i <= n;i++)
        {
            scanf("%d",&node[i].len);
            node[i].l = ;
            for(int j = ;j < i;j++)
                node[i].l = max(node[i].l,node[j].r - abs(node[i].len - node[j].len));
            node[i].r = node[i].l + *node[i].len;
        }
        for(int i = ;i <= n;i++)
        {
            for(int j = ;j < i;j++)
                if(node[i].l < node[j].r && node[i].len < node[j].len)
                     node[i].l = node[j].r;
            for(int j = i+;j <= n;j++)
                if(node[i].r > node[j].l && node[i].len < node[j].len)
                     node[i].r = node[j].l;
        }
        bool first = true;
        for(int i = ;i <= n;i++)
            if(node[i].l < node[i].r)
        {
            if(first)first = false;
            else printf(" ");
            printf("%d",i);
        }
        printf("\n");
    }
    return ;
}