洛谷 P3195 [HNOI2008] 玩具装箱

链接：

P3195

---

题意：

给出 \(n\) 个物品及其权值 \(c\)，连续的物品可以放进一个容器，如果将 \(i\sim j\) 的物品放进一个容器，产生的费用是 \(\left(j-i+\sum\limits_{k=i}^jc_k-L\right)^2\)，其中 \(L\) 是一个给出的常数，现在需要把所有物品都放进容器，请你最小化总费用。

---

分析：

这是一道非常经典的好题，适合练习单调队列优化和斜率优化dp。

我们设 \(sum[i]\) 表示物品权值的前缀和，\(dp[i]\) 表示前 \(i\) 个物品的最小总费用，那么有 \(O(n)\) 转移：

\[dp[i]=\min \left(dp[j]+(i-(j+1)+sum[i]-sum[j]-L)^2\right)
\]

我们将后面的式子化一下，把与 \(i\) 有关的和与 \(j\) 有关的拉出来,常数项随意丢进里面，

\[dp[i]=dp[j]+( (i+sum[i])-(j+sum[j]+L+1) )^2
\]

令 \(A(i)=i+sum[i],B(j)=j+sum[j]+L+1\)

\[dp[i]=dp[j]+A(i)^2-2A(i)B(j)+B(j)^2
\]

我们发现 \(A(i)\) 和 \(B(j)\) 都是已知的，而 \(A(i)\) 只与当前位置有关，\(B(j)\) 只与之前的位置有关，可以视为决策。

由于存在 \(A(i)B(j)\) 这种既与当前位置有关，又与决策有关的东西，于是我们尝试将与决策有关的东西单独分离出来。我们对这个式子进行变换：

\[dp[j]+B(j)^2=2A(i)B(j)+dp[i]-A(i)^2
\]

可以将其视为一条斜率为 \(2A(i)\) 的直线，经过定点 \((B(j),dp[j]+B(j)^2)\)，截距为 \(dp[i]-A(i)^2\)。

我们成功将决策的信息与整合到了一个点上！现在需要做的就是选择一个最优的点，使得一条斜率一定的直线经过这个点时截距最小。

图片摘自洛谷博客

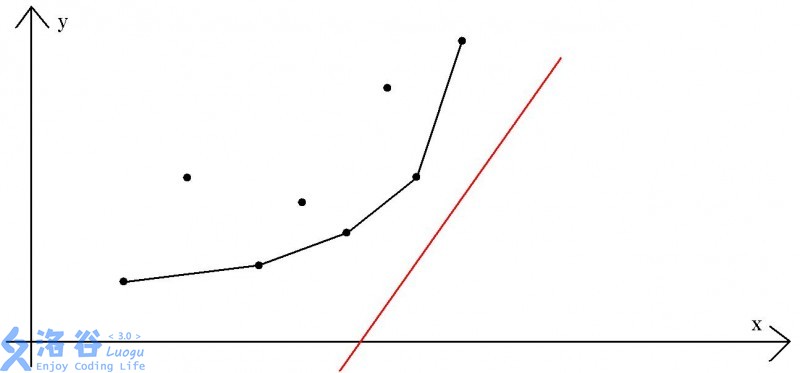
我们通过观察可以发现，可能作为最优决策的点构成了一个下凸包（这在其他题目中可能不同），且对于一条斜率为 \(k\) 的直线，最优决策点是第一个满足 \(slope(x,x+1)\geq k\) 的点。（\(slope\) 表示斜率）

用单调队列维护凸包。同时注意到每次询问的斜率 \(2A(i)\) 也是单调增的，于是对于找到最优决策点还可以用单调队列优化。

注意到一个细节是要 "插入第0个点" 的信息，否则无法将 \(1\sim i\) 放进一个容器。

---

算法：

单调队列维护下凸包，同时维护最优决策点，然后每次根据最优决策的信息得到 \(dp[i]\)，继续维护凸包即可。时间复杂度 \(O(n)\)。

---

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=5e4+5;
#define A(x) (x+sum[x])
#define B(x) (x+sum[x]+1+L)
#define X(x) (B(x))
#define Y(x) (dp[x]+B(x)*B(x))
#define dx(x,y) (X(x)-X(y))
#define dy(x,y) (Y(x)-Y(y))
#define slope(x,y)(double(dy(x,y))/dx(x,y))
int n,L,sum[N],dp[N],q[N],qi=1,qn=1;
signed main(){
	n=in,L=in;
	for(int i=1;i<=n;i++)
		sum[i]=sum[i-1]+in;
	for(int i=1;i<=n;i++){
		while(qi<qn&&slope(q[qi+1],q[qi])<2*A(i))qi++;
		dp[i]=dp[q[qi]]+(A(i)-B(q[qi]))*(A(i)-B(q[qi]));
		while(qn>qi&&slope(q[qn],q[qn-1])>slope(i,q[qn-1]))qn--;
		q[++qn]=i;
	}
	cout<<dp[n];
	return 0;
}

题外话：

真的是一道极好的斜优入门题。