[学习笔记] MRF 入门

MRF马尔可夫随机场入门

Intro

MRF是一种广泛应用于图像分割的模型，当然我看到MRF的时候并不是因为分割，而是在图像生成领域，有的paper利用MRF模型来生成图像，因此入门一下MRF，并以分割模型为例记一下代码。

Model

Target

在图像分割中，我们的任务是给定一张图像，输出每个像素的标签。因此我们就是要得到在给定图片特征之下，标签概率最大化时所对应的标签。

因此可以这么建模：

\[\hat{\omega} = arg \max_{\omega \in \Omega} P(\omega|f)
\]

其中w表示标签，f表示图像特征，求最大后验概率。

根据贝叶斯理论，上式右边可以写成：

\[P(\omega|f) = \frac{P(f|\omega)P(\omega)}{P(f)}
\]

其中，P(f)是常量，因为当一张图片确定之后，P(f)便确定了。因此，上式只取决于分子部分。分子又可以表达为\(P(f,\omega)\)，所以我们直接建模的其实是这个部分，计算的也是这个部分，这是与CRF不同的一点(MRF是直接对左边建模，不分解为右边，所以没个样本都要算一遍后验概率，然后乘起来最大化，MRF其实是通过对等式右边分子建模"曲线救国")。

因此，我们的任务中只需要对分子的两个部分进行定义即可。

Neighbors

像素Neighbors的定义很简单，就是这个像素周围的其他像素。

举例而言，下图分别是中心点像素的四邻域和八邻域。

Hammersley-Clifford Theorem

定理的内容为：

如果一个分布\(P(x)>0\)满足无向图\(G\)中的局部马尔可夫性质，当且仅当\(P(x)\)可以表示为一系列定义在最大团上的非负函数的乘积形式，即：

\[P(x) = \frac{1}{Z} \prod_{c \in C} \phi (x_c)
\]

其中\(C\)为\(G\)中最大团集合，也就是所有的最大团组成的集合，\(\phi(x_c) \ge 0\)是定义在团\(c\)上的势能函数，Z是配分函数，用来将乘积归一化为概率的形式。

\[Z = \sum_{x \in \Chi } \prod_{c \in C} \phi (x_c)
\]

无向图模型与有向图模型的一个重要区别就是配分函数Z。

Hammersley-Clifford Theorem表明，无向图模型和吉布斯分布是一致的，所以将\(P(\omega)\)定义下式：

\[P(\omega) = \frac{1}{Z}exp(-U(\omega)) = \frac{1}{Z}exp(- \sum_{c \in C} V_c(\omega))
\]

其中，Z作为normalization项，\(Z = \sum exp(-U(\omega))\)，U定义为势能，而等号最右边将U变成了V的求和，在后面我们会说到，这里其实是每个原子团的势能的求和。

Clique

Clique就是我们上面提到的“团”的概念。集合\(c\)是\(S\)的原子团当且仅当c中的每个元素都与该集合中的其他元素相邻。那么Clique就是所有\(c\)的并集。

\[C = c_1 \cup c_2 \cdots c_n
\]

举例而言：

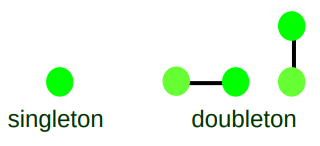
一个像素的四邻域及他自己组成的集合的原子团可以分为singleton和doubleton如图所示。

Clique Potential

翻译过来就是势能，用\(V(w)\)表示，描述的是一个Clique的能量。

那么，一个像素的领域的势能就是每个团的能量的和。

\[U(\omega) = \sum_{c \in C} V_c(w)
\]

其中c表示原子团,c表示Clique，V是如何定义的呢？

在图像分割中，可以以一阶团为例，

\[V_c(\omega) = \beta \delta(w,w_s) = \left\{\begin{aligned} -\beta &&w = w_s \\\beta && w \neq w_s \\\end{aligned}\right.
\]

到这里，\(P(\omega)\)的所有变量解释完了，下一步是计算\(P(f|\omega)\)

\(P(f|\omega)\)的计算

\(P(f|\omega)\)被认为是服从高斯分布的，也就是说，如果我们知道了这个像素的标签是什么，那么他的像素值应该服从这个标签下的条件概率的高斯分布。其实他服从高斯分布还是很好理解的，我们已知这个像素点的label比如说是A，那么我们去统计一下所有标签是A的点的像素值的均值和方差，显然以这个均值和方差为参数的高斯分布更加契合这里的条件分布。

\[P(f_s|\omega_s) = \frac{1}{\sqrt{2\pi}\sigma_{w_s}}exp(-\frac{(f_s - \mu_{\omega_s})^2}{2\sigma^2_{\omega_s}})
\]

计算每个类别的像素均值和方差，带入公式，即得条件概率。

最后，就是最大化\(P(\omega)P(f|\omega)\),以对数形式转化为求和的形式去优化，最大化\(log(P(\omega)) + log(P(f|\omega))\).

Coding

import numpy as np
import cv2 as cv
import copy
class MRF():
    def __init__(self,img,max_iter = 100,num_clusters = 5,init_func = None,beta = 8e-4):
        self.max_iter = max_iter
        self.kernels = np.zeros(shape = (8,3,3))
        self.beta = beta
        self.num_clusters = num_clusters
        for i in range(9):
            if i < 4:
                self.kernels[i,i//3,i%3] = 1
            elif i > 4:
                self.kernels[i-1,i//3,i%3] = 1
        self.img = img
        if init_func is None:
            self.labels = np.random.randint(low = 1,high = num_clusters + 1,size = img.shape,dtype = np.uint8)

    def __call__(self):
        img = self.img.reshape((-1,))
        for iter in range(self.max_iter):
            p1 = np.zeros(shape = (self.num_clusters,self.img.shape[0] * self.img.shape[1]))
            for cluster_idx in range(self.num_clusters):
                temp = np.zeros(shape = (self.img.shape))
                for i in range(8):
                    res = cv.filter2D(self.labels,-1,self.kernels[i,:,:])
                    temp[(res == (cluster_idx + 1))] -= self.beta
                    temp[(res != (cluster_idx + 1))] += self.beta
                temp = np.exp(-temp)
                p1[cluster_idx,:] = temp.reshape((-1,))
            p1 = p1 / np.sum(p1)
            p1[p1 == 0] = 1e-3
            mu = np.zeros(shape = (self.num_clusters,))
            sigma = np.zeros(shape = (self.num_clusters,))
            for i in range(self.num_clusters):
                #mu[i] = np.mean(self.img[self.labels == (i+1)])
                data = self.img[self.labels == (i+1)]
                if np.sum(data) > 0:
                    mu[i] = np.mean(data)
                    sigma[i] = np.var(data)
                else:
                    mu[i]= 0
                    sigma[i] = 1
                #print(sigma[i])
            #sigma[sigma == 0] = 1e-3
            p2 = np.zeros(shape = (self.num_clusters,self.img.shape[0] * self.img.shape[1]))
            for i in range(self.img.shape[0] * self.img.shape[1]):
               for j in range(self.num_clusters):
                   #print(sigma[j])
                   p2[j,i] = -np.log(np.sqrt(2*np.pi)*sigma[j]) -(img[i]-mu[j])**2/2/sigma[j];
            self.labels = np.argmax(np.log(p1) + p2,axis = 0) + 1
            self.labels = np.reshape(self.labels,self.img.shape).astype(np.uint8)
            print("-----------start-----------")
            print(p1)
            print("-" * 20)
            print(p2)
            print("----------end------------")
            #print("iter {} over!".format(iter))
            #self.show()
            #print(self.labels)
    def show(self):
        h,w = self.img.shape
        show_img = np.zeros(shape = (h,w,3),dtype = np.uint8)
        show_img[self.labels == 1,:] = (0,255,255)
        show_img[self.labels == 2,:] = (220,20,60)
        show_img[self.labels == 3,:] = (65,105,225)
        show_img[self.labels == 4,:] = (50,205,50)
        #img = self.labels / (self.num_clusters) * 255

        cv.imshow("res",show_img)
        cv.waitKey(0)
if __name__ == "__main__":
    img = cv.imread("/home/xueaoru/图片/0.jpg")

    img = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
    img = img/255.
    #img = np.random.rand(64,64)
    #img = cv.resize(img,(256,256))
    mrf = MRF(img = img,max_iter = 20,num_clusters = 2)
    mrf()
    mrf.show()
    #print(mrf.kernels)

Input:

Output(num_clusters = 4):

Output(num_clusters = 2):