#LOF算法

a.每个数据点，计算它与其他点的距离

b.找到它的K近邻，计算LOF得分

clf=LocalOutlierFactor(n_neighbors=20,algorithm='auto',contamination=0.1,n_jobs=-1,p=2)

参数含义

●n_neighbors=20:即LOF算法中的k的值，检测的邻域点个数超过样本数则使用所有的样本进行检测

●algorithm = 'auto'：使用的求解算法，使用默认值即可

●contamination = 0.1：范围为 (0, 0.5)，表示样本中的异常点比例，默认为 0.1

● n_jobs = -1：并行任务数，设置为-1表示使用所有CPU进行工作

● p = 2：距离度量函数，默认使用欧式距离。

def localoutlierfactor(data, predict, k):
    from sklearn.neighbors import LocalOutlierFactor
    clf = LocalOutlierFactor(n_neighbors=k + 1, algorithm='auto', contamination=0.1, n_jobs=-1)
    clf.fit(data)
    # 记录 k 邻域距离
    predict['k distances'] = clf.kneighbors(predict)[0].max(axis=1)
    # 记录 LOF 离群因子，做相反数处理
    predict['local outlier factor'] = -clf._decision_function(predict.iloc[:, :-1])
    return predict

def plot_lof(result, method):
    import matplotlib.pyplot as plt
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    plt.figure(figsize=(8, 4)).add_subplot(111)
    plt.scatter(result[result['local outlier factor'] > method].index,
                result[result['local outlier factor'] > method]['local outlier factor'], c='red', s=50,
                marker='.', alpha=None,
                label='离群点')
    plt.scatter(result[result['local outlier factor'] <= method].index,
                result[result['local outlier factor'] <= method]['local outlier factor'], c='black', s=50,
                marker='.', alpha=None, label='正常点')
    plt.hlines(method, -2, 2 + max(result.index), linestyles='--')
    plt.xlim(-2, 2 + max(result.index))
    plt.title('LOF局部离群点检测', fontsize=13)
    plt.ylabel('局部离群因子', fontsize=15)
    plt.legend()
    plt.show()

def lof(data, predict=None, k=5, method=1, plot=True):
    import pandas as pd
    # 判断是否传入测试数据，若没有传入则测试数据赋值为训练数据
    try:
        if predict == None:
            predict = data.copy()
    except Exception:
        pass
    predict = pd.DataFrame(predict)
    # 计算 LOF 离群因子
    predict = localoutlierfactor(data, predict, k)
    if plot == True:
        plot_lof(predict, method)
    # 根据阈值划分离群点与正常点
    outliers = predict[predict['local outlier factor'] > method].sort_values(by='local outlier factor')
    inliers = predict[predict['local outlier factor'] <= method].sort_values(by='local outlier factor')
    return outliers, inliers

import numpy as np
import pandas as pd
import xlrd
# 根据文件位置自行修改
posi = pd.read_excel(r'./已结束项目任务数据.xls')
lon = np.array(posi["任务gps经度"][:])  # 经度
lat = np.array(posi["任务gps 纬度"][:])  # 纬度
A = list(zip(lat, lon))  # 按照纬度-经度匹配

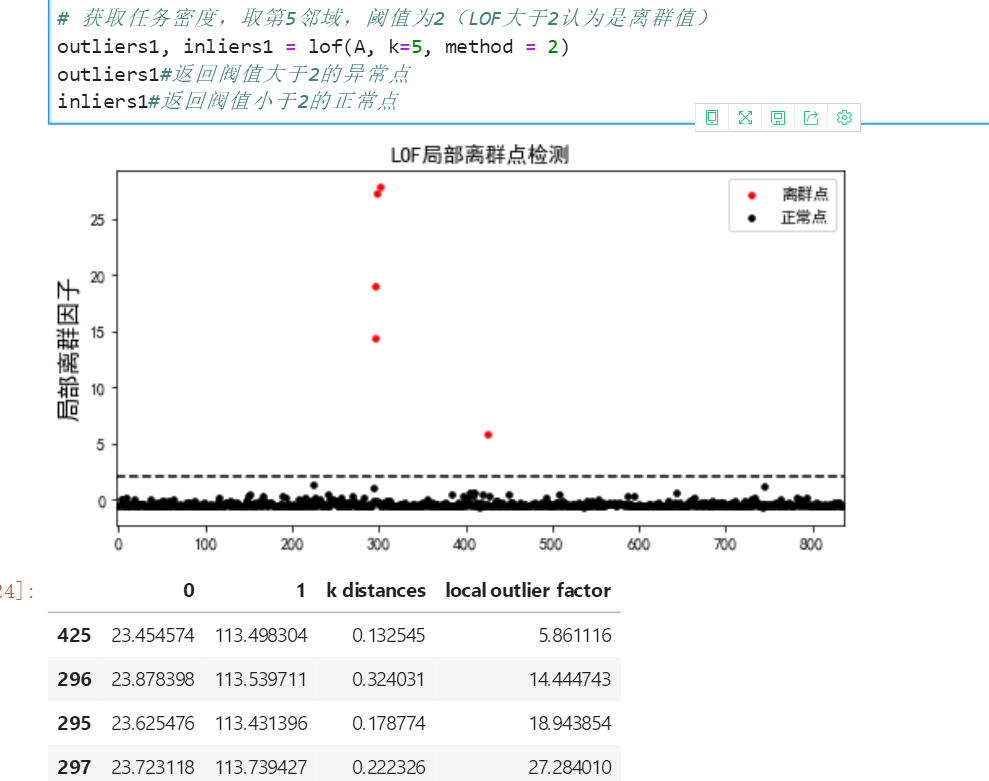
# 获取任务密度，取第5邻域，阈值为2（LOF大于2认为是离群值）
outliers1, inliers1 = lof(A, k=5, method = 2)

参考链接：

https://www.jianshu.com/p/8c5c0c903f27

https://zhuanlan.zhihu.com/p/28178476

异常检测的几种方法

https://xz.aliyun.com/t/5378