「WC 2018」州区划分

题目大意：

　　给一个无向图$G(V,E)$满足$|V|<=21$，对于某一种将$G(V,E)$划分为k个的有序集合方案，若每一个子集$G_i(V_i,E_i)$，$E_i=\{(x,y)|x\in V_i,y\in V_i\}$都不存在欧拉回路，则会对答案贡献为

　　　

　　其中，$x$为集合元素，$w_x$为元素$x$的权值。

题解：

　　被题意坑成Cu……我还是太菜了……

　　其实很显然我们会得到一个$DP$，设$F_S$为集合$S$划分后的乘积和。

　　显然我们有转移方程：

　　　　

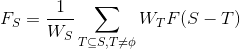
　　$W_S$表示$[G(S,E_S)不存在欧拉回路](\sum_{x\in S}w_x)^P$

　　一个裸的子集卷积的式子。

　　时间复杂度$n^2 2^n$

代码：

　　

#include "bits/stdc++.h"

using namespace std;

inline int read () {
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}

const int mod = 998244353,N=1<<21;

inline int powmod (int a,int b) {
    int ret=1;
    while (b) {
        if (b&1) ret=ret*1ll*a%mod;
        b>>=1,a=a*1ll*a%mod;
    }return ret;
}

inline void add (int &x,int y) {
    x+=y;
    if (x>=mod) x-=mod;
}

inline void erase (int &x,int y) {
    x-=y;
    if (x<0) x+=mod;
}

inline void FWT (int *a,int n,int f) {
    register int i,j,k;
    if (f)
        for (i=1;i<n;i<<=1)
            for (j=0;j<n;j+=i<<1)
                for (k=0;k<i;++k)  {
                    int x=a[j+k],y=a[i+j+k];
                    erase(y,x);
                    a[i+j+k] = y;
                }
    else
        for (i=1;i<n;i<<=1)
            for (j=0;j<n;j+=i<<1)
                for (k=0;k<i;++k)  {
                    int x=a[j+k],y=a[i+j+k];
                    add(y,x);
                    a[i+j+k] = y;
                }
}

int f[22][N],g[22][N],n,m,p,fa[21],w[N],num[N],inv[N],v[N];
int mp[N];

inline int calc (int x) {
    if (!p) return 1;
    if (p&1) return x;
    return x*x;
}

int finds (int x) {
    return fa[x]==x?x:fa[x]=finds(fa[x]);
}

inline int check(int S) {
    register int i,j;
    static int d[21];
    for (i=0;i<n;++i)   if (S&(1<<i)) fa[i]=i,d[i]=0;
    j=num[S];
    for (i=0;i<n;++i)
        if (S&(1<<i))   {
            for (int x=v[i]&S,t;x;x^=x&-x){
                ++d[i];
                t=mp[x&-x];
                ++d[t];
                if (finds(i)^finds(t))fa[fa[i]]=fa[t],--j;
            }
        }
    if (j>1) return true;
    for (i=0;i<n;++i)   if (S&(1<<i)) if (d[i]&1)return true;
    return false;
}

inline void add(int *a,int *b,int *c) {
    for (register int i=0;i<(1<<n);++i)
        add(a[i],b[i]*1ll*c[i]%mod);
}

int main () {
    n=read(),m=read(),p=read();

    register int i,j,k;

    for (i=0;i<m;++i) {
        int x=read()-1,y=read()-1;
        v[x]|=1<<y;
    }
    int S=1<<n;
    for (i=0;i<n;++i)
        w[1<<i]=read(),mp[1<<i]=i;
    for (i=2;i<S;i<<=1)
        for (j=1,k=w[i];j<i;++j) {
            int x=w[j];
            x=x+k;
            w[i|j] = x;
        }
    for (i=1;i<S;++i) {
        num[i] = num[i>>1]+(i&1);
        int tmp=w[i];
        tmp=calc(tmp);
        g[num[i]][i] = check(i) * tmp;
        inv[i] = powmod(tmp,mod-2);
    }
    for (i=0;i<S;++i)
        f[0][i]=1;

    for (i=1;i<=n;++i)
        FWT(g[i],S,0),
        memcpy(f[i],g[i],sizeof f[i]);
    for (i=1;i<=n;++i) {
        for (j=1;j<i;++j)
            for (k=0;k<S;++k) {
                int x=f[i][k],y=g[j][k],z=f[i-j][k];
                add(x,1ll*y*z%mod);
                f[i][k]=x;
            }
        FWT(f[i],S,1);
        for (j=0;j<S;++j)   {
            int x=f[i][j],y=inv[j];
            x=x*1ll*y%mod;
            f[i][j] = x;
        }
        if (i^n) FWT(f[i],S,0);
    }
    printf("%d\n",f[n][S-1]);
}