XGBoost算法--学习笔记

学习背景

最近想要学习和实现一下XGBoost算法，原因是最近对项目有些想法，准备做个回归预测。作为当下比较火的回归预测算法，准备直接套用试试效果。

一、基础知识

（1）泰勒公式

泰勒公式是一个用函数在某点的信息描述其附近取值的公式。具有局部有效性。

基本形式如下：

由以上的基本形式可知泰勒公式的迭代形式为：

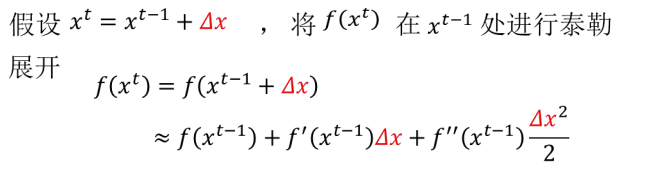
以上这个迭代形式是针对二阶泰勒展开，你也可以进行更多阶的泰勒展开。

（2）梯度下降法

在机器学习算法中，我们的目标是最小化损失函数L(theta), 结合泰勒展开公式，我们可以得到如下的公式：

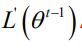为什么这里的, 我觉得是因为这样它和前面的相乘之后，只要a取正值，那么他的变化值就一定是一个负数，换句话，这样就能够确保他的损失一定是减少的。

（3）牛顿法

牛顿法和梯度下降法一样都是一种优化手段。他们二者的区别在于牛顿法采用的二阶泰勒展开，而梯度下降使用的一阶泰勒展开。

二、概念解释

（1）gradient descend和gradient boosting

　　gradient descend和gradient boosting的区别在于前者是对于参数的更新，后者是对于模型的更新

（2）Boosting算法

Boosting算法是一种加法模型：

（3）决策树

决策树的优点：可解释性，可处理混合类型特征，具有伸缩不变形，具有特征组合的作用，可自然的处理缺失值，对异常点鲁棒， 有特征选择作用，可拓展性强，容易并行

决策树的缺点：缺乏平滑性（针对回归树）， 不适合处理高维稀疏数据

三、GBDT算法

XGBoost算法是GBDT算法的进阶版，在我们了解和实现XGBoost算法之前，要先了解GBDT算法。